Electricidad/Campo eléctrico/Campo eléctrico generado por una distribución discreta de cargas

El concepto de campo electrostático facilita la descripción, en términos físicos, de la influencia que una o más cargas eléctricas ejercen sobre el espacio que les rodea. Para un grupo de cargas puntuales puede ser calculado cómo se indica.

Caso general

Para determinar el campo eléctrico producido por un conjunto de cargas puntuales se calcula el campo debido a cada carga en el punto dado como si fuera la única carga que existiera y se suman vectorialmente los mismos para encontrar el campo resultante en el punto. En forma de ecuación:

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2+{\overrightarrow{E}}_3+...+{\overrightarrow{E}}_n=\sum _{i=1}^n{\overrightarrow{E}}_i=\sum _{i=1}^n\frac{1}{4\pi {ϵ}_0{r}_i^2}{\overrightarrow{u_r}}_i$

Campo eléctrico creado por un dipolo eléctrico

A continuación se analiza el campo eléctrico creado por una distribución de dos cargas de igual magnitud y de signo opuesto conocida como Dipolo eléctrico

A. Campo eléctrico en los puntos de la bisectriz del eje del dipolo

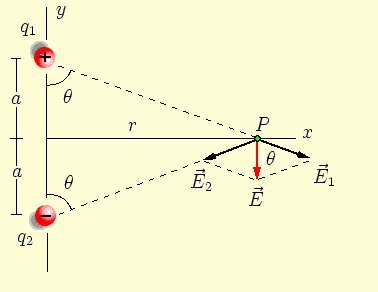
Según el principio de superposición, el campo eléctrico en el punto $P$ es la suma vectorial de los dos campos creados por ambas cargas:

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2$

Por el teorema de Pitágoras se cumple que la distancia entre cualquiera de las cargas y el punto $P$ es:

$\sqrt{a^2+r^2}$

Y como ambas cargas son de igual magnitud se cumple:

$E_1=E_2=\frac{1}{4\pi {ϵ}_0}\frac{q}{a^2+r^2}$

Las componentes $E_{1_x}$ y $E_{2_x}$ poseen la misma magnitud pero apuntan en sentidos opuestos, por lo tanto:

$E_{1_x}+E_{2_x}=0$

En consecuencia, para efectuar la suma vectorial, sólo se deberán tener en cuenta a las componentes $E_y$, es decir, la suma vectorial de ${\overrightarrow{E}}_1$ y ${\overrightarrow{E}}_2$ apuntan verticalmente hacia abajo, y siendo $E_{1_y}=E_{2_y}$, se cumplirá que:

$E=2E_1\cos \theta$

Teniendo en cuenta que:

$\cos \theta =\frac{a}{\sqrt{a^2+r^2}}$

y sustituyendo esta expresión y la de $E_1$ en la expresión de $E$ se obtiene:

$E=\frac{2}{4\pi ϵ}\frac{q}{a^2+r^2}\frac{a}{\sqrt{a^2+r^2}}=\frac{1}{4\pi ϵ}\frac{2aq}{(a^2+r^2{)}^{\frac{3}{2}}}$

Si $r$ >> $a$ se puede omitir a $a$ en el denominador y la ecuación se reduce a:

$E\approx \frac{1}{4\pi ϵ}\frac{(2a)(q)}{r^3}$

El producto $2aq$ se denomina momento $p$ del dipolo eléctrico. Entonces, se puede volver a escribir la ecuación de $E$ como:

$E=\frac{1}{4\pi ϵ}\frac{p}{(a^2+r^2{)}^{\frac{3}{2}}}$

Y si r>>a, es decir, para puntos distantes a lo largo de la bisectriz del eje del dipolo como:

$E\approx \frac{1}{4\pi ϵ}\frac{p}{r^3}$

B. Campo eléctrico en los puntos del eje del dipolo

Puntos fuera de la línea de unión de las cargas

Como en el caso anterior, según el principio de superposición, el campo eléctrico en el punto $P$ es la suma vectorial de los campos creados por ambas cargas.

$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2$

Se observa que, al estar ambos vectores sobre el eje $x$, se cumple:

$E_{1_y}=E_{2_y}=0$

Por tanto, a efectos de calcular la suma vectorial, solo deben tenerse en cuenta las componentes $E_{1_x}$ y $E_{2_x}$.

En consecuencia las magnitudes del campo debidas a $q_1$ y $q_2$ serán respectivamente:

$E_1=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r-a)}^2}{E}_2=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r+a)}^2}$

Como ambas componentes, $E_{1_x}$ y $E_{2_x}$, apuntan en sentidos contrarios:

$E=E_1-E_2$

O sea:

$E=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r-a)}^2}-\frac{1}{4\pi {ϵ}_0}\frac{q}{{(r+a)}^2}=\frac{1}{4\pi {ϵ}_0}[\frac{q}{{(r-a)}^2}-\frac{q}{{(r+a)}^2}]=\frac{1}{4\pi {ϵ}_0}4aq\frac{r}{{(r^2-a^2)}^2}$

Siendo $p=2aq$ el momento del dipolo eléctrico:

$E=\frac{1}{2\pi {ϵ}_0}\frac{pr}{{(r^2-a^2)}^2}$

Y si $r$ >> $a$:

$E\approx \frac{1}{2\pi {ϵ}_0}\frac{p}{r^3}$

Puntos sobre la línea de unión de las cargas

La magnitud de $\overrightarrow{E}$ para puntos ubicados entre las cargas, tales como el punto $Q$, puede deducirse mediante un razonamiento similar al anterior. La diferencia estriba en que las componentes, $E_{1_x}$ y $E_{2_x}$, apuntan en el mismo sentido y por ello se suman en lugar de restarse:

$E=E_1+E_2$

Siendo:

$E_1=\frac{1}{4\pi {ϵ}_0}\frac{q}{l^2}{E}_2=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(2a-l)}^2}$

Por tanto:

$E=\frac{1}{4\pi {ϵ}_0}\frac{q}{l^2}+\frac{1}{4\pi {ϵ}_0}\frac{q}{{(2a-l)}^2}=\frac{1}{4\pi {ϵ}_0}[\frac{q}{l^2}+\frac{q}{{(2a-l)}^2}]=\frac{1}{4\pi {ϵ}_0}q\frac{2a}{l^2(2a-l)}$

Siendo $p=2aq$ el momento del dipolo eléctrico:

$E=\frac{1}{4\pi {ϵ}_0}\frac{p}{l^2(2a-l)}$

C. Otros puntos

Considérese un dipolo eléctrico y un punto $P$ de coordenadas $(x,y)$ tal como el representado en la figura.

Se cumple que:

$r_1=\sqrt{{(y+a)}^2+x^2}\cos \alpha =\frac{y+a}{\sqrt{{(y+a)}^2+x^2}}\sin \alpha =\frac{x}{\sqrt{{(y+a)}^2+x^2}}$

$r_2=\sqrt{{(y-a)}^2+x^2}\cos \beta =\frac{y-a}{\sqrt{{(y-a)}^2+x^2}}\sin \beta =\frac{x}{\sqrt{{(y-a)}^2+x^2}}$

En base a lo anterior, los campos generados por cada carga serán:

${E_r}_1=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y+a)}^2+x^2}{E_r}_2=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(y-a)}^2+x^2}$

Para determinar el campo en $P$ se aplica el principio de superposición por lo cual se debe efectuar la suma vectorial de los campos creados por ambas cargas.

Se calculan, entonces, las componentes $x$:

${{E_r}_1}_x=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y+a)}^2+x^2}\sin \alpha =\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y+a)}^2+x^2}\frac{x}{\sqrt{{(y+a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{-qx}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}$

${{E_r}_2}_x=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(y-a)}^2+x^2}\sin \beta =\frac{1}{4\pi {ϵ}_0}\frac{q}{{(y-a)}^2+x^2}\frac{x}{\sqrt{{y-a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{qx}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}$

Las componentes $y$ serán:

${{E_r}_1}_y=\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y+a)}^2+x^2}\cos \alpha =\frac{1}{4\pi {ϵ}_0}\frac{-q}{{(y+a)}^2+x^2}\frac{y+a}{\sqrt{{(y+a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{-q(y+a)}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}$

${{E_r}_2}_y=\frac{1}{4\pi {ϵ}_0}\frac{q}{{(y-a)}^2+x^2}\cos \beta =\frac{1}{4\pi {ϵ}_0}\frac{q}{{(y-a)}^2+x^2}\frac{y-a}{\sqrt{{y-a)}^2+x^2}}=\frac{1}{4\pi {ϵ}_0}\frac{q(y-a)}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}$

Sumando se obtiene para la componente $x$ total:

$E_x=\frac{1}{4\pi {ϵ}_0}q[\frac{x}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}-\frac{x}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}]$

Y para la componente $y$ total:

$E_y=\frac{1}{4\pi {ϵ}_0}q[\frac{y-a}{{[{(y-a)}^2+x^2]}^{\frac{3}{2}}}-\frac{y+a}{{[{(y+a)}^2+x^2]}^{\frac{3}{2}}}]$

Los denominadores de las expresiones anteriores pueden ser escritos en forma compacta como:

$\frac{1}{{[{(y\mp a)}^2+x^2]}^{\frac{3}{2}}}=\frac{1}{{[y^2\mp 2ay+a^2+x^2]}^{\frac{3}{2}}}=\frac{1}{{[x^2+y^2\mp 2ay+a^2]}^{\frac{3}{2}}}=\frac{1}{{[r^2\mp 2ay+a^2]}^{\frac{3}{2}}}$

Si se consideran puntos alejados del dipolo, entonces, $r>>a\Rightarrow r^2>>a^2$ con lo cual se puede despreciar el término $a^2$ y en consecuencia se obtiene:

$\frac{1}{{[r^2\mp 2ay+a^2]}^{\frac{3}{2}}}\approx \frac{1}{{[r^2\mp 2ay]}^{\frac{3}{2}}}=\frac{1}{{\left[r^2(1\mp \frac{2ay}{r^2})\right]}^{\frac{3}{2}}}=\frac{1}{r^3}{(1\mp \frac{2ay}{r^2})}^{-\frac{3}{2}}$

Aplicando el Teorema del binomio y tomando los dos primeros términos del desarrollo:

${(1\mp \frac{2ay}{r^2})}^{-\frac{3}{2}}\approx 1-\frac{3}{2}(\mp \frac{2ay}{r^2})=1\pm \frac{3ay}{r^2}$

En consecuencia:

$\frac{1}{{[{(y\mp a)}^2+x^2]}^{\frac{3}{2}}}\approx \frac{1}{r^3}(1\pm \frac{3ay}{r^2})$

Si se sustituye este resultado en las expresiones de las componentes, se obtiene:

$E_x\approx \frac{1}{4\pi {ϵ}_0}qx[\frac{1}{r^3}(1+\frac{3ay}{r^2})-\frac{1}{r^3}(1-\frac{3ay}{r^2})]$

$E_y\approx \frac{1}{4\pi {ϵ}_0}q[(y-a)\frac{1}{r^3}(1+\frac{3ay}{r^2})-(y+a)\frac{1}{r^3}(1-\frac{3ay}{r^2})]$

Operando apropiadamente y teniendo en cuenta que $2aq=p$, se obtiene para puntos alejados del diplo:

$E_x\approx \frac{1}{4\pi {ϵ}_0}\frac{3pxy}{{(x^2+y^2)}^{\frac{5}{2}}}{E}_y\approx \frac{1}{4\pi {ϵ}_0}\frac{p(2y^2-x^2)}{{(x^2+y^2)}^{\frac{5}{2}}}$

Campo generado por un cuadrupolo eléctrico lineal en su bisectriz

Un cuadrupolo eléctrico lineal es una distribución de cargas formada por dos dipolos alineados de forma opuesta de manera tal que sus cargas positivas se encuentran superpuestas y cuyas cargas producen una fuerza 0 entre ellas debido a su posicion. (Ver figura).

Para determinar el campo eléctrico producido por el cuadrupolo sobre los puntos pertenecientes a su bisectriz, de acuerdo al principio de superposición, se deben sumar las contribuciones debidas a las cargas positivas y las producidas por las negativas.

El campo producido por cada carga positiva será: $E_q=\frac{q}{4\pi {ϵ}_o{r}^2}$

Obsérvese que las componentes paralelas al cuadrupolo serán nulas, por lo tanto el campo total producido por ambas cargas positivas será: $E_{2q}=\frac{2q}{4\pi {ϵ}_o{r}^2}$

El campo producido por cada carga negativa será: $E_{-q}=\frac{-q}{4\pi {ϵ}_o(r^2+d^2)}$

Por simetría, las componentes paralelas al cuadrupolo, se cancelan, por lo tanto, sólo deben ser tenidas en cuanta las componentes colineales con la bisectriz.

Teniendo en cuenta que

$\sin \theta =\frac{r}{\sqrt{r^2+d^2}}$

, el valor de cada componente colineal con la bisectriz será:

$E_{-q}=\frac{-q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

y el aporte total correspondiente a ambas cargas negativas será: $E_{-2q}=\frac{-2q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

Por lo tanto, el campo total será: $E=E_{2q}+E_{-2q}=\frac{2q}{4\pi {ϵ}_o{r}^2}+\frac{-2q}{4\pi {ϵ}_o(r^2+d^2)}\frac{r}{\sqrt{r^2+d^2}}$

O sea:

$E=\frac{q}{2\pi {ϵ}_0}[\frac{1}{r^2}-\frac{r}{{(r^2+d^2)}^{\frac{3}{2}}}]$

Si se saca $\frac{1}{r^2}$ de factor común, la expresión anterior se puede expresar como:

$E=\frac{q}{2\pi {ϵ}_0{r}^2}[1-{(1+\frac{d^2}{r^2})}^{-\frac{3}{2}}]$

Si se consideran puntos alejados del cuadrupolo, se cumple que $r>>d\Rightarrow r^2>>d^2\Rightarrow \frac{d^2}{r^2}<<1$ y por lo tanto aplicando el Teorema del binomio se verifica que :

${(1+\frac{d^2}{r^2})}^{-\frac{3}{2}}\approx 1-\frac{3}{2}\frac{d^2}{r^2}$

Con lo cual. la expresión de campo eléctrico para los puntos alejados del cuadrupolo se reduce a:

$E\approx \frac{3Q}{4\pi {ϵ}_0{r}^4}$

Donde $Q=q{d}^2$ se conoce como momento de cuadrupolo.

Véase también

• Campo eléctrico generado por una distribución continua lineal de carga
• Campo eléctrico generado por una distribución continua superficial de carga
• Campo eléctrico generado por una distribución continua volumétrica de carga
• Campo electrostático
• Carga eléctrica
• Ley de Coulomb
• Ley de Gauss
• Potencial eléctrico