Problemario de Señales y Sistemas/Señales Periódicas

Señales Periódicas

En esta serie de problemas se busca que el estudiante se familiarice con el concepto período, frecuencia y suma de señales periódicas (cuando son señales sinusoidales, ¿puede extenderse a la multiplicación?.

Problemas

Problema 2 02 08

Para las señales que se listan a continuación determine cuáles son periódicas y cuáles no. Para las señales periódicas calcule su período y frecuencia (rad/s), su área absoluta, energía, potencia y valor RMS en un período. En todos los casos grafique la señal en el intervalo -6<t<6. Si hubiera señales complejas grafique parte real e imaginaria.

1. $y_1(t)=\sin \left(\frac{\pi }{3}t\right)+\sin \left(\frac{2\pi }{5}t\right)+\sin (2\pi t+\frac{\pi }{6})+\cos (10\pi t+\frac{\pi }{3})$
2. $y_2(t)=\sin (2t)+(10+2i)\cos (2\pi t)+e^{jt}$
3. $y_3(t)=\sin (2\pi t)+\sin (\sqrt{2}\pi t)$

Problema #1

Para las señales que se listan a continuación determine cuáles son periódicas y cuáles no. Para las señales periódicas calcule su período y frecuencia (rad/s), su área absoluta, energía, potencia y valor RMS en un período. En todos los casos grafique la señal en el intervalo -6<t<6. Si hubiera señales complejas grafique parte real e imaginaria.

1. $x_1(t)=\sin \left(\frac{1}{3}t\right)+\cos (\frac{1}{2}t+\frac{\pi }{5})+\sin (2t+2)$
2. $x_2(t)=\sin (2\pi t)+e^{j5\pi t}$
3. $x_3(t)=\sin (3t)+\sin (\sqrt{3}t)+\sin (3\sqrt{3}t)$

Problema #1. Subproblema 1=

Realizado por Esteban Bacilio 05-37871

1. $x_1(t)=\sin \left(\frac{1}{3}t\right)+\cos (\frac{1}{2}t+\frac{\pi }{5})+\sin (2t+2)$

Se tienen w1=1/3; w2=1/2; w3=2;. Se puede ver que la razón de cualquier par de frecuencias individuales es una fracción racional => la señal es periódica.

La frecuencia natural wn es el MCD de las frecuencias individuales: wn=MCD(1/3,1/2,2)=1/6 rad/seg.

El período natural correspondiente Tn=2$\pi ,$/wn=2$\pi ,$/(1/6)=12$\pi ,$

La Potencia de la señal X1(t) es la suma de las potencias individuales:

$P=P_1+P_2+P_3=\frac{1}{Tn}\underset{0}{\overset{Tn}{\int }}\sin \left(\frac{1}{3}t\right)dt+\frac{1}{Tn}\underset{0}{\overset{Tn}{\int }}\cos (\frac{1}{2}t+\frac{\pi }{5})dt+\frac{1}{Tn}\underset{0}{\overset{Tn}{\int }}\sin (2t+2)dt=\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{3}{2}[W]$

El valor rms de la señal: $x_{rms}=\sqrt{(P)}=\sqrt{\frac{3}{2}}$

Entonces la energía en un período Tn: $E=Tn.P=18[J]$

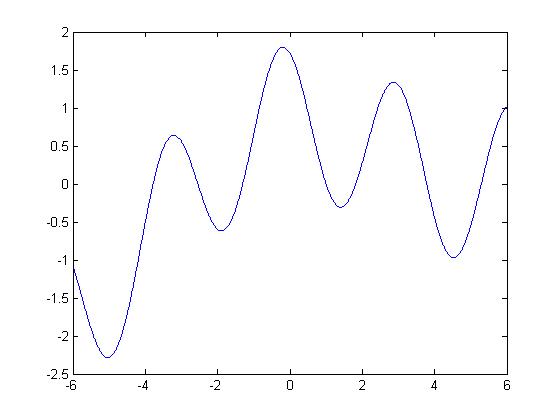
La gráfica de esta señal es la siguiente:

a) Para un tiempo entre -6 < t < 6

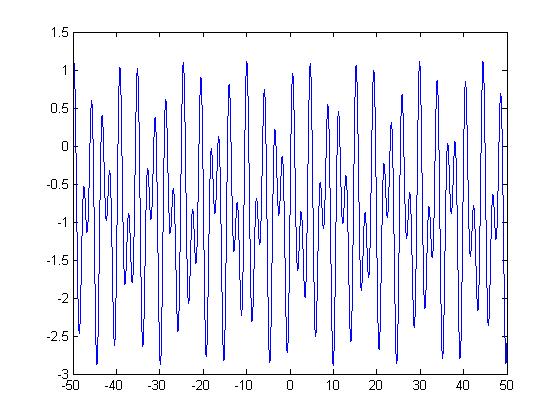
b) Para un tiempo entre -80 < t < 80 ( En donde podemos apreciar la frecuencia y periodo fundamental.

Problema #1. Subproblema 2=

Realizado por Esteban Bacilio 05-37871

1. $x_2(t)=\sin (2\pi t)+e^{j5\pi t}$

como $x_2(t)=e^{j5\pi t}=\cos (5\pi t)+j\cdot \sin (5\pi t)$

nos queda: $\sin (2\pi t)+\cos (5\pi t)+j\cdot \sin (5\pi t)$

Parte real. Se tienen w1=2 y w2=5, entonces, como la razón de ambas frecuencias es un número racional: w1/w2=2/5 => la parte real de la señal es periódica.

La frecuencia natural wn de la parte real: $w_n=MCD(5\pi ,2\pi )=\pi$ El período, Tn=2.

La Potencia de esta señal en un período Tn es la suma de las potencias individuales:

$P=P_1+P_2=\frac{1}{Tn}\underset{0}{\overset{Tn}{\int }}\sin (2\pi t)dt+\frac{1}{Tn}\underset{0}{\overset{Tn}{\int }}\cos (5\pi t)dt=\frac{1}{2}+\frac{1}{2}=1[W]$

El valor rms de la señal (para la parte real): $x_{rms}=\sqrt{(P)}=1$

La energía en un período Tn: $E=Tn.P=2[J]$

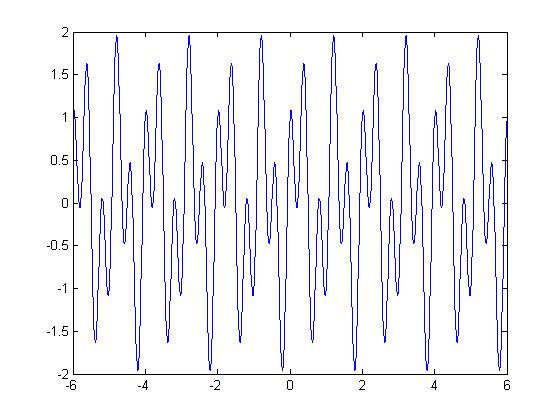
La gráfica de la parte real de la función para un intervalo de tiempo entre -6 < t < 6:

Parte imaginaria. La señal está dada por un solo seno => es periódica

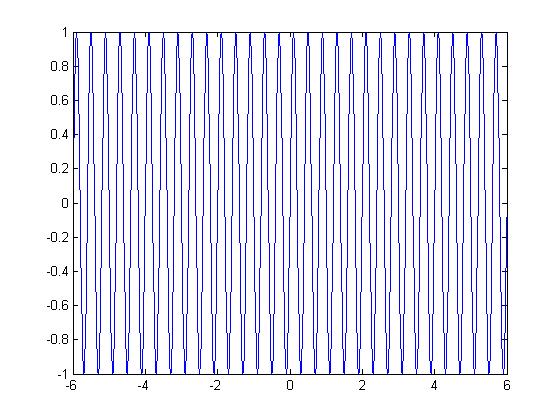
La gráfica de la parte imaginaria:

Problema #1. Subproblema 3

Realizado por Euro Rivero 03-36396

1. $x_3(t)=\sin (3t)+\sin (\sqrt{3}t)+\sin (3\sqrt{3}t)$

Se tienen las frecuencias individuales: w1=3 w2=$\sqrt{3}$ w3=$3\sqrt{3}$

La razón entre un par de frecuencias: w1/w2= $3/\sqrt{3}$ nos da un número no racional => la señal no es periódica.

La gráfica de esta señal es: