Problemario de Señales y Sistemas/Operaciones con Señales

Operaciones con Señales

En esta sección colocamos problemas sobre operaciones con señales (suma, resta, multiplicación y, cuando se pueda, división) y operaciones sobre la variable independiente.

Problemas

Problema 1 02 08

Considere las siguientes señales fundamentales: $u(t)=\{\begin{array}{cc}1& t>0\\ 0& t<0\end{array}$; $r_a(t)=\{\begin{array}{cc}t& t>0\\ 0& t<0\end{array}$; $x(t)=\{\begin{array}{cc}\sin (2\pi t)& 0<t<1\\ 0& t<0;t>1\end{array}$;

Realice las siguientes operaciones y grafique sus respuestas. En cada caso calcule Promedio, Área Absoluta, Energía y Potencia:

1. $x_1(t)=u(t+0.5)u(0.5-t)$
2. $x_2(t)=r_a(t+1)-2r_a(t)+r_a(t-1)$
3. $x_3(t)=\sum _{n=-K}^K{x}_1(t-2n)$, con K=3. ¿Qué sucede cuando K tiende a infinito?
4. $x_4(t)=\sum _{n=-K}^K{x}_2(t-nT)$, con K=3 y T=2. ¿Qué sucede cuando K tiende a infinito?.
5. Repita el problema anterior con T=1.
6. $x_6(t)=\sum _{n=-(K-1)}^{K}x(t+n)$, con K=3.
7. $x_7(t)=x_6(t)x_3(t)$
8. $x_8(t)=\sum _{n=3}^3{x}_6(2n)x_1(t-2n)$. Compare las señales x7 y x8. ¿Cuál es la diferencia?

---

Solucion Problema 1.1 y 1.2

a) # $x_1(t)=u(t-1)u(2-t)$. (Resuelto por Gilfredo Remon 06-40153).

La grafica de la señal es:

1. $Valorpromedio={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}u(t+0.5)u(0.5-t)dt$.
2. $Areaabsoluta={\int }_{-0.5}^{0.5}u(t+0.5)u(0.5-t)dt=1\ast 1=1$.
3. $Energia={\int }_{-0.5}^{0.5}|u(t+0.5)u(0.5-t){|}^{2}dt=1$.
4. $Potencia=1{\int }_{-0.5}^{0.5}|u(t+0.5)u(0.5-t){|}^{2}dt$.

b) # $x_2(t)=r_a(t+1)-2r_a(t)+r_a(t-1)$. (Resuelto por: JABG 06-40153).

La grafica es:

1. $x_{pro}=0$.
2. $Area={\int }_{-1}^{0}t+1dt+{\int }_0^1-t+1dt=1$.
3. $Energia={\int }_{-1}^0|t+1{|}^{2}dt+{\int }_0^1|1-t{|}^{2}dt=0$.(Corregido por F.Omar)
4. $Potencia=\frac{1}{2}[{\int }_{-1}^0|t+1{|}^{2}dt+{\int }_0^1|1-t{|}^{2}dt]=\frac{1}{6}$.
5. $Potenci{a}_{\mathrm{\infty }}=0$.

Problema 3 02 08

Considere la señal $x_9(t)=u(t+5)u(5-t)$, y sea $z(t)=x_9(t)+x_2(t);$, $z_1(t)=z(t-5).$. Calcule y grafique las partes pares e impares de z1(t).

Realizado por: Adriana Carolina Corredor. Carnet 06-39396

Toda señal puede ser representada como la suma de su parte par más su parte impar $X(t)=X_e(t)+X_o(t)$

Para $X_2(t)=r_a(t-1)-2r_a(t)+r_a(t-1)$

Parte Par: $X(t)=X(-t)$

Por lo que, la parte par sera: $0,5(X_2(t))+0,5(X_2(-t))$

Como se puede observar en esta señal, la parte par es igual a la señal como tal, siendo la parte impar $X_o(t)=0,5((X_2(t))-0,5((X_2(-t))=0$

LA SEÑAL ES COMPLETAMENTE PAR

---

Para $X_9(t)=u(t+5)u(5-t)$

Archivo:Imagen4.jpg

Parte Par: $X(t)=X(-t)$

Por lo que, la parte par sera: $0,5(X_9(t))+0,5(X_9(-t))$

Como se puede observar en esta señal, la parte par es igual a la señal como tal, siendo la parte impar $X_o(t)=0,5((X_9(t))-0,5((X_9(-t))=0$

LA SEÑAL ES COMPLETAMENTE PAR

---

Para $Z(t)=X_9(t)+X_2(t)$

Parte Par: $X(t)=X(-t)$

Como esta señal es la suma de dos señales pares, entonces esta señal debe ser par. Claro que se puede observar que $Z(t)=Z(-t)$ y que la parte impar es cero.

Como se puede observar en esta señal, la parte par es igual a la señal como tal, siendo la parte impar $X_o(t)=0,5((Z(t))-0,5((Z(-t))=0$

LA SEÑAL ES COMPLETAMENTE PAR

---

---

Por: Daniel Sanchez 06-40306

La parte par es: $z{1}_{par}(t)=0,5[u(t+10)u(10-t)+r_a(t-4)-2r_a(t-5)+r_a(t-6)+r_a(t+6)-2r_a(t+5)+r_a(t+4)]$

La parte impar es: $z{1}_{impar}(t)=0,5[-u(t+10)+2u(t)-u(t-10)+r_a(t-4)-2r_a(t-5)+r_a(t-6)-r_a(t+6)+2r_a(t+5)-r_a(t+4)]$

Las graficas son: Parte Par

Parte Impar

Problema 4 02 08

Para las señales que se listan a continuación, indique cuáles son de energía y cuáles de potencia (en el caso de que lo fueran).

1. $q_1(t)=\frac{1}{1+t^2}$
2. $q_2(t)=1+\cos (\pi t)u(t)$

Problema 5 02 08

Evalúe las siguientes operaciones:

1. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(4-t^2)\delta (t+3)dt$
2. $y_4(t)={\int }_{-\mathrm{\infty }}^t[4-{\tau }^2]\delta (\tau +3)d\tau$
3. ${\int }_{-3}^6(6-t^2)[\delta (t+4)+2\delta (2t+4)]dt$
4. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[e^{-5t}+\cos (10\pi t)]\dot{\delta }(t)dt$
5. $y_5(t)={\int }_{-\mathrm{\infty }}^t[e^{-5\tau }+\cos (10\pi \tau )]\dot{\delta }(\tau )d\tau$.

Solucion del Problema # 5: Marianela Mendoza 06-39906.

Estas operaciones se resolvieron aplicando propiedades del impulso y el doblete. Impulso: Las integrales que llevan impulsos multiplicando funciones son sencillas de resolver, esto se debe a sus propiedades.

1. $\delta (t-t_o).f(t)=\delta (t-t_o).f(t_o)$
2. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\delta (t-t_o).f(t)]dt=f(t_o).{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-t_o)dt=f(t_o)$
3. $\delta (b(t-t_o))=\frac{\delta (t-t_o)}{\left|b\right|}$ siendo b cualquier numero.

De la manera siguiente se obtuvieron los resultados: Procedimeinto: Se multiplica la delta por la funcion (es decir, evalua la funcion en donde existe la delta), y luego, lo que queda es una constante multiplicando la delta, finalmente la integral de lo que queda es esa constante, tal como se muestra en los ejercicios.

1. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(4-t^2)\delta (t+3)dt=-5{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t+3)dt=-5$.
2. $y_4(t)={\int }_{-\mathrm{\infty }}^t[4-{\tau }^2]\delta (\tau +3)d\tau =5{\int }_{-\mathrm{\infty }}^t\delta (\tau +3)d\tau ;y_4(t)=5,(t>3)$.
3. ${\int }_{-3}^6(6-t^2)[\delta (t+4)+2\delta (2t+4)]dt={\int }_{-3}^6-10\delta (t+4)+2\delta (t+2)dt=2$.

Doblete: Propiedades del doblete, mostradas a continuacion son las herramientas que se utilizaron para la resolucion de las siguientes integrales.

1. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\dot{\delta }(t)]dt=0$
2. $\dot{\delta }(t).f(t)=\dot{\delta }(t).f(o)-\dot{f}(t).\delta (t)$
3. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\dot{\delta }(t).f(t)]dt={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\dot{\delta }(t).f(o)]dt-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\dot{f}(t).\delta (t)]dt=-\dot{f}(o)$
4. $\dot{\delta }(bt)=\frac{\delta (t)}{b\left|b\right|}$ siendo b cualquier numero.

Igual que en la parte anterior, aplicando estas propiedades se resuelven las integrales.

1. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[e^{-5t}+\cos (10\pi t)]\dot{\delta }(t)dt=5$.
2. $y_5(t)={\int }_{-\mathrm{\infty }}^t[e^{-5\tau }+\cos (10\pi \tau )]\dot{\delta }(\tau )d\tau ={\int }_{-\mathrm{\infty }}^{t}2\dot{\delta }(\tau )+5\delta (t)d\tau =5(t=0);0(t\ne 0)$.

Problema 1

En un sistema lineal e invariante en el tiempo, la relación entre la entrada ($x(t)$) y la salida ($y(t)$) es:

$y(t)={\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}x(-0.5\tau +1)d\tau$

Determine:

1. La respuesta al impulso ($\delta (t)$) del sistema.
2. La respuesta al pulso (${\mathrm{\Pi }}_1(t)$): Amplitud 1, centrado en el origen y duración 1).

---

Solución Problema 1

Propuesta de solucion: Damian Vigouroux 17/05/2007 05-39044

Parte 1.

 $h(t)={\int }_{-\mathrm{\infty }}^t{e}^{-(t-\tau )}\delta (-0.5\tau +1)d\tau$ Trabajando con el impulso: $\delta (-0.5\tau +1)=\delta (-0.5(\tau -2))=2\delta (\tau -2)$

Por lo tanto : $e^{-(t-\tau )}\delta (-0.5\tau +1)=2e^{-(t-\tau )}\delta (\tau -2)=2e^{-(t-2)}\delta (\tau -2)$ ... usando las propiedades del impulso

Entonces la respuesta al impulso será: $h(t)={\int }_{-\mathrm{\infty }}^{t}2e^{-(t-2)}\delta (\tau -2)d\tau =2e^{-(t-2)}{\int }_{-\mathrm{\infty }}^t\delta (\tau -2)d\tau =2e^{-(t-2)}u(t-2)$

Parte 2. Conociendo la respuesta al impulso del sistema (LTI) podemos carecterizar su comportamiento ante cualquier señar de entrada específicamente a: ${\mathrm{\Pi }}_1(t)$

$y(t)=x(t)\ast h(t)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x(\tau )h(t-\tau )d\tau$ En este caso $x(t)={\mathrm{\Pi }}_1(t)=1$ si t E(-0.5,0.5) y cero para todo lo demás

Sea t < 1.5

Un análisis gráfico del producto $y(t)=x(\tau ).h(t-\tau )$ muestra que y(t) es cero

Sea 1.5 < t < 2.5

En este caso $y(t)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x(\tau )h(t-\tau )d\tau ={\int }_{-0.5}^{t-2}2e^{-(t-\tau -2)}d\tau =2e^{-(t-2)}{\int }_{-0.5}^{t-2}{e}^{\tau }d\tau =2(1-e^{-(t-1.5)})$

Sea 2.5 > t

Definiendo la region común, distinta de cero de las gráficas: $y(t)={\int }_{-0.5}^{0.5}2e^{-(t-\tau -2)}d\tau =2e^{-(t-2)}{\int }_{-0.5}^{0.5}{e}^{\tau }d\tau =2(e^{0.5}-e^{-0.5})e^{-(t-2)}$

Luego la respuesta a $x(t)={\mathrm{\Pi }}_1(t)$ del sistema será la unión de y(t) en los tres intervalos anteriores.

---

Problema 2

Repita el problema anterior si la relación entrada salida cambia a:

$y(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-(t-\tau )}x(-0.5\tau +1)d\tau$

---

Solución Problema 2

Realizado por: José Velásquez #05-39032

1) Tenemos que la respuesta al impulso ($\delta (t)$) del sistema esta dada por:

$h(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-(t-\tau )}\delta (-0.5\tau +1)d\tau$

Comenzamos empleando las propiedades del impulso para determinar $h(t)$:

Por la propiedad de escalamiento del impulso se tiene que:

$\delta [\alpha (t-\beta )]=\left|\frac{1}{\alpha }\right|\delta (t-\beta )$

Entonces,

$h(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}2e^{-(t-\tau )}\delta (\tau -2)d\tau$

Utilizando la propiedad de filtrado del impulso:

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t)\delta (t-\alpha )dt=x(\alpha )$

De esta manera,

$h(t)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}2e^{-(t-\tau )}\delta (\tau -2)d\tau =2e^{-(t-2)}$

2) Tenemos que la respuesta al pulso ${\mathrm{\Pi }}_1(t)$ (amplitud 1, centrado en el origen y duración 1) esta da por:

$y(t)=x(t)\ast h(t)=h(t)\ast x(t)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}h(\tau )x(t-\tau )d\tau$ (Propiedad conmutativa de la convolución)

$y(t)={\int }_{t-0.5}^{t+0.5}2e^{-(\tau -2)}d\tau =2(e^{2.5}-e^{1.5})e^{-t}$

Siendo $y(t)=2(e^{2.5}-e^{1.5})e^{-t}\mathrm{\forall }t\in (-\mathrm{\infty },+\mathrm{\infty })$ la respuesta del sistema al pulso ${\mathrm{\Pi }}_1(t)$ inicialmente mencionado.

---

Problema 3

Considere el sistema modulador que se muestra en la figura, en el que la moduladora es $g(t)=\sin (2\pi t)$

Determine la respuesta del sistema ($y(t)$) cuando en la entrada se aplica:

1. $x(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-4k)$
2. $x(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{\Pi }}_1(t-8k)$

Solución Problema 3

Realizado por: José Velásquez #05-39032

1) La respuesta del sistema (y(t)) cuando en la entrada se aplica:

$x(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-4k)$

Teniendo en cuenta la señal moduladora,

$g(t)=\sin (2\pi t)$

Empleando la propiedad del producto del impulso:

${}_{}{X}_I(t)=X(t)\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-k{}_{}{t}_s)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}X(k{}_{}{t}_s)\delta (t-k{}_{}{t}_s)$

Se obtiene entonces,

$y(t)=g(t)x(t)=\sin (2\pi t)\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-4k)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\sin (2\pi 4k)\delta (t-4k)$

$y(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\sin (8\pi k)\delta (t-4k)$

Esto se trata de un tren de impulsos cuyas intensidades estan dadas por la señal moduladora $g(t)=\sin (2\pi t)$ evaluada en $t=4k\mathrm{\forall }k(entero)\in (-\mathrm{\infty },+\mathrm{\infty })$

2) La respuesta del sistema (y(t)) cuando en la entrada se aplica:

$x(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{\Pi }}_1(t-8k)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}[u(t-8k+0.5)-u(t-8k-0.5)]$

Teniendo en cuenta la misma señal moduladora,

$y(t)=g(t)x(t)=\sin (2\pi t)\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}[u(t-8k+0.5)-u(t-8k-0.5)]$

${}_{}{\omega }_o=2\pi /T$

$T=\frac{2\pi }{{\omega }_o}\Rightarrow T=1$

A partir de esto y de un análisis gráfico,

$y(t)=\sin (2\pi t)si8k-0.5\le t\le 8k+0.5\mathrm{\forall }k(entero)\in (-\mathrm{\infty },+\mathrm{\infty })$

Esto representa un tren de senoides de ancho 1 y período igual a 8.

---

Problema 4

Considere las señales $x(t)=\frac{e^{-\frac{t^2}{8}}}{2\sqrt{2\pi }}$, $t\in (-\mathrm{\infty },\mathrm{\infty })$ y

$\mathrm{\Pi }(t)=\{\begin{array}{cc}0& t<-0.1\\ 1& -0.1\le t\le 0.1\\ 0& t>0.1\end{array}$

y sea

$y(t)=\sum _{k=-6}^{6}x(kT)\mathrm{\Pi }(t-kT)$

Calcule y grafique $x(t),\mathrm{\Pi }(t),y(t)$ cuando

1. T=1
2. T=0.2

---

Solución 1 Problema 4

Realizado por: Jesús Querales #05-38758

1. $T=1$

• La señal $x(t)$ tiene forma de curva gaussiana y su valor en t=0 es $\frac{1}{2\sqrt{2\pi }}\approx 0.2$

La gráfica de $x(t)$ se muestra en la siguiente figura:

• El pulso $\mathrm{\Pi }(t)=u(t+0.1)-u(t-0.1)$ tiene altura 1 y ancho 0.2, representado en la siguiente figura:

Archivo:Fig2 problema4.gif

• La señal $y(t)=\sum _{k=-6}^{6}x(k)\mathrm{\Pi }(t-k)$

Donde,

$x(k)=\frac{e^{-\frac{k^2}{8}}}{2\sqrt{2\pi }}$ y

$\mathrm{\Pi }(t-k)=u(t-k+0.1)-u(t-k-0.1)$

Luego,

$y(t)=\sum _{k=-6}^6\frac{e^{-\frac{k^2}{8}}}{2\sqrt{2\pi }}[u(t-k+0.1)-u(t-k-0.1)]$

Se representa en la siguiente figura:

Problema 5

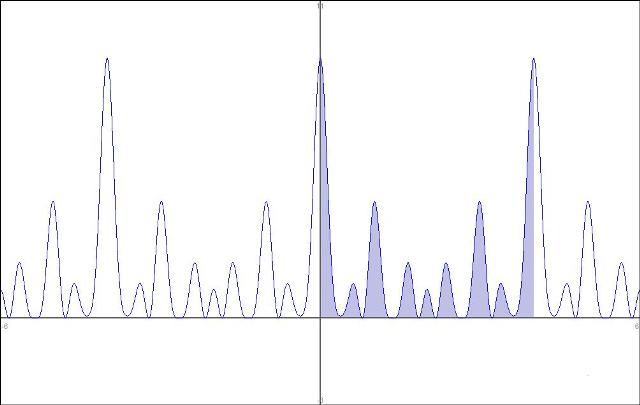
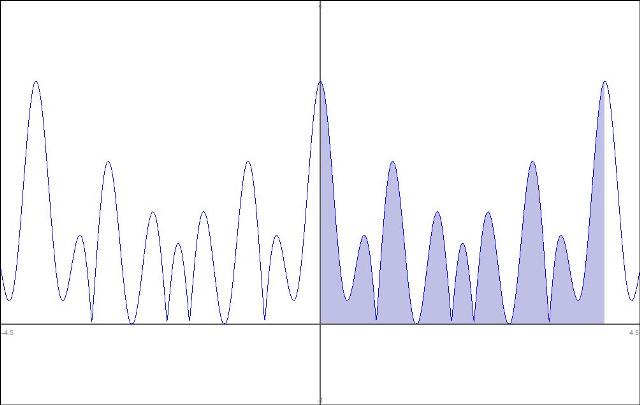
Considere la señal $x(t)=\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t)$, calcule:

1. La frecuencia y el período fundamentales
2. La energía, potencia, promedio, valor RMS y área absoluta en un período

Solución Problema 5

Realizado por: José Velásquez #05-39032

1. La frecuencia fundamental está dada por:

${\omega }_o=GCD(\frac{\pi }{2},\pi ,3\pi )=\frac{\pi }{2}$

De esto, el período fundamental resulta:

$T=\frac{2\pi }{{\omega }_o}\Rightarrow T=\frac{2\pi }{\frac{\pi }{2}}=4$

2. Para el análisis y la compresión de esta parte se presentan tres gráficas ilustrativas. En cada imagen se sombrea el área debajo la curva en un período $\text{T}$.

$x(t)=\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t)$

$x_1(t)=[\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t){]}^2$

$x_2(t)=|\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t)|$

• La Energía en un período viene dada por:

${}_{}{E}_x={\int }_T{|x(t)|}^{2}dt={\int }_0^4[\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t){]}^{2}dt=6$

• La Potencia en un período viene dada por:

${}_{}{P}_x=\frac{1}{T}{\int }_T{|x(t)|}^{2}dt=\frac{{}_{}{E}_x}{T}=\frac{6}{4}=\frac{3}{2}$

• El Promedio en un período viene dado por:

${}_{}{X}_{\text{pro}}=\frac{1}{T}{\int }_{T}x(t)dt={\int }_0^4[\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t)]dt=0$

• El valor RMS viene dado por:

${}_{}{X}_{\text{rms}}=\sqrt[]{{}_{}{P}_x}=\sqrt[]{\frac{3}{2}}$

Y finalmente el Área absoluta viene dada por:

${}_{}{A}_{\text{abs}}=\frac{1}{T}{\int }_T|x(t)|dt=\frac{1}{4}{\int }_0^4|\cos (\frac{\pi }{2}t)+\cos (\pi t)+\cos (3\pi t)|dt=\frac{3,9847}{4}=0,996$

Problema 6

Evalúe las siguientes expresiones:

1. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(5-8t^2)\delta (-3t-9)dt$
2. $x(t)={\int }_{-\mathrm{\infty }}^t(5-8{\tau }^2)\delta (-3\tau -9)d\tau$
3. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[e^{-5t}-\sin (5\pi t)]\dot{\delta }(-2t+8)dt$
4. $x(t)={\int }_{-\mathrm{\infty }}^t[e^{-5\tau }-\sin (5\pi \tau )]\dot{\delta }(-2\tau +8)d\tau$

Solución Problema 6

Realizado por: Orlando Díaz #05-38117

1)

Utilizando las propiedades de la $\delta (t)$ tenemos que:

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(5-8t^2)\delta (-3t-9)dt=\frac{1}{3}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(5-8t^2)\delta (t+3)dt$

Luego, la propiedad de filtrado de $\delta (t)$ es:

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t)\delta (t-\alpha )dt=x(\alpha )$

Utilizando esta propiedad en el problema resulta en que:

$\frac{1}{3}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(5-8t^2)\delta (t+3)dt=\frac{1}{3}(5-8(-3{)}^2)=-\frac{67}{3}$

2)

Trabajaremos primero con la parte interna de la integral, por propiedades obtenemos:

$(5-8{\tau }^2)\delta (-3\tau -9)=\frac{1}{3}(5-8{\tau }^2)\delta (\tau +3)$

Analicemos el resultado, $\delta (t)$ es una función que es $0$ para $t\ne o$ y $1$ para $t=0$, por tanto $\delta (\tau +3)$ solo existe en $\tau =-3$. Al multiplicar esta función por $(5-8{\tau }^2)$ implica simplemente producir un $\delta (\tau )$ cuya altura es el valor de $x(\tau )$ en $\tau =-3$. Por tanto nos queda.:

$\frac{1}{3}(5-8(-3{)}^2)\delta (\tau +3)=\frac{-67}{3}\delta (\tau +3)$

Así que, nuestra integral original resulta en:

${\int }_{-\mathrm{\infty }}^t\frac{-67}{3}\delta (\tau +3)d\tau =\frac{-67}{3}{\int }_{-\mathrm{\infty }}^t\delta (\tau +3)d\tau$

El impulso es la derivada de la función escalón, así que la integral de un impulso es un escalón que comienza donde existe el impulso, por tanto la respuesta es:

${\int }_{-\mathrm{\infty }}^t\frac{1}{3}(5-8{\tau }^2)\delta (\tau +3)d\tau =\frac{-67}{3}U(t+3)$

3)

El doblete ${\delta }^{\prime }(t)$ esta definido como la derivada del impulso. Si trabajamos con sus propiedades obtendremos:

$[e^{-5t}-sen(5\pi t)]{\delta }^{\prime }(-2t+8)=\frac{1}{-4}[e^{-5t}-sen(5\pi t)]{\delta }^{\prime }(t-4)$

La propiedad de filtrado del doblete nos dice que:

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t){\delta }^{\prime }(t-\alpha )dt=-x^{\prime }(\alpha )$

Aplicándolo en nuestro problema hayamos la solución:

$\frac{1}{-4}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[e^{-5t}-\sin (5\pi t)]\dot{\delta }(t-4)dt=-\frac{1}{4}[-5e^{-5t}-5\pi cos(5\pi t){]}_{T=4}=\frac{5e^{-20}}{4}+\frac{5\pi }{4}$

4)

Realizado por Julio Aguilar Carnet: 06-39117

El doblete ${\delta }^{\prime }(t)$ esta definido de la siguiente manera:

cero (0) para todo "t" distinto de cero y

${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\delta }^{\prime }(t)dt=0$

Sus propiedades son las siguientes:

(1)$x(t){\delta }^{\prime }(t-\alpha )=x(\alpha ){\delta }^{\prime }(t-\alpha )-x(\alpha {)}^{\prime }\delta (t-\alpha )$

(2)${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}x(t){\delta }^{\prime }(t-\alpha )dt=-x^{\prime }(\alpha )$

(3)${\delta }^{\prime }(at+b)=\frac{1}{a|a|}{\delta }^{\prime }(t+\frac{b}{a})$

Aplicando la tercera propiedad se tiene que:

$[e^{-5t}-sen(5\pi t)]{\delta }^{\prime }(-2t+8)=\frac{1}{-4}[e^{-5t}-sen(5\pi t)]{\delta }^{\prime }(t-4)$

y luego la primera propiedad tenemos que:

$\frac{1}{-4}[e^{-5t}-sen(5\pi t)]{\delta }^{\prime }(t-4)=\frac{e^{-20}}{-4}{\delta }^{\prime }(t-4)-[\frac{-5e^{-20}-5\pi }{4}]\delta (t-4)$

Integrando y aplicando la definicion se tiene que la primera parte es igual a cero:

${\int }_{-\mathrm{\infty }}^t{\delta }^{\prime }(t-4)=0$

La segunda parte queda:

${\int }_{-\mathrm{\infty }}^t[\frac{5e^{-20}+5\pi }{4}]\delta (t-4)=[\frac{5e^{-20}+5\pi }{4}]U(t-4)$