Problemario de Señales y Sistemas/Muestreo de señales y respuesta de sistemas LTI

---

Problemas

Problema #1

Considere el sistema que se muestra en el que la señal de entrada, $x(t)$, es muestreada con un tren de pulsos $p(t)$ para producir la señal $z(t)=(x(t)p(t))$. La señal $z(t)$ pasa a través de un sistema lineal invariante en el tiempo cuya respuesta el impulso es $h(t)$.

Se desea que determine y grafique el par: $(z(t),y(t))$.

En este caso $x(t)=\cos (2\pi t)$, $h(t)=3e^{-5t}u(t)$ y $p(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-0.5n)$

Nota: Para efectos de la solución, puede suponer que, $h(t)=0$ $\mathrm{\forall }t\ge t_1$, donde $h(t_1)=0.1h(0)$. Igualmente $H(j\omega )=0\mathrm{\forall }\omega \ge {\omega }_1$, donde $|H(j{\omega }_1)|=0.1|H(j0)|$. Esto es, que, para todo fin práctico, la respuesta al impulso y la respuesta en frecuencia del sistema se consideran cero cuando alcanzan el 10% de su valor en cero.

Subsección solución 1

Hecho por: Pedro Torruella #04-37657

1) Primero elijo trabajar sobre la base de la frecuencia, ya que por las propiedades de la transformada de Fourier puedo hacer los cálculos fácilmente.

Primero convierto

$x(t)=cos(2\pi t)(1)$

Que por propiedades de la transformada de fourier queda como:

$X(j\omega )=\pi (\delta (\omega -2\pi )+\delta (\omega +2\pi ))(2)$

Luego transformo

$p(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-0.5n)(3)$

que por tablas obtenemos

$P(j\omega )=4\pi \sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -k4\pi )$

Al convolucionar con la función $X\left(j\omega \right)$ obtenemos unos deltas con módulos de $4{\pi }^2$ de la siguiente forma

$Z(j\omega )=4{\pi }^2\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -k4\pi -2\pi )+\delta (\omega -k4\pi +2\pi )$

o lo que es lo mismo

$Z(j\omega )=8{\pi }^2\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (\omega -k2\pi )-\delta (\omega -k4\pi )$

Al convertir $Z(j\omega )$ al dominio del tiempo por las tablas de transformadas, obtenemos un tren de pulsos

$z(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}4\delta (t-k)-2\delta (t-k\frac{1}{2}\pi )$

Para obtener y(t) tengo que convolucionar z(t) con h(t). Como z(t) es un tren de impulsos, lo que voy a obtener es una repetición de h(t) por cada pulso, por otro lado, los pulsos tienen un espaciado de 0,5, como h(t) es nula para valores mayores a 0,46 unidades de tiempo, una no se sobrepone con la otra cuando se convoluciona con el tren de pulsos, por lo tanto obtendremos algo como esto:

$y(t)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}12e^{-5(t-k)}-6e^{-5(t-k\frac{1}{2}\pi )}$

Subsección solución 2

Por: Alejandro González 04-37066

Trabajando en la base del tiempo, se tiene para $z(t)$:

$z(t)=\cos (2\pi t)\cdot \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\delta (t-0.5n)$

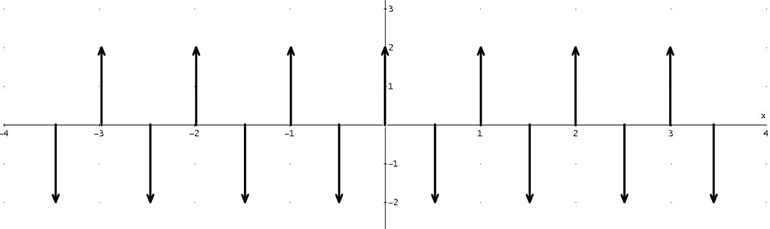
Esto, gráficamente, es algo así:

Archivo:Tren de pulsos por coseno.png

Esta función se puede reescribir como:

$z(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(-1{)}^n\cdot \delta (t-0.5n)$

Con la suposición, $h(t)=0$ $\mathrm{\forall }t\ge t_1$, donde $h(t_1)=0.1h(0)$

se calcula $t_1$:

$h(0)=3e^0=3$

luego, $h(t_1)=0.1h(0)=0.3$

finalmente:

$3e^{-5t_1}=0.3\Rightarrow -5t_1=ln(0.1)\Rightarrow t_1\approx 0.46$

y se puede reescribir $h(t)$ como: $h(t)=3e^{-5t}u(t)u(0.46-t)$

Ahora, convolucionando la función $z(t)$ con la función $h(t)$, se tiene:

$\begin{array}{ccc}y(t)& =& z(t)*h(t)\\ & =& h(t)*z(t)\\ & =& \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}(3e^{-5\tau }u(\tau )u(0.46-\tau ))\cdot (\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(-1{)}^n\cdot \delta (t-\tau -0.5n))d\tau \end{array}$

$y(t)=3\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(-1{)}^n\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{e}^{-5\tau }u(\tau )u(0.46-\tau )\delta (t-\tau -0.5n)d\tau$

finalmente:

$y(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(-1{)}^{n}3e^{-5t+2.5n}u(t-0.5n)u(0.46+0.5n-t)$

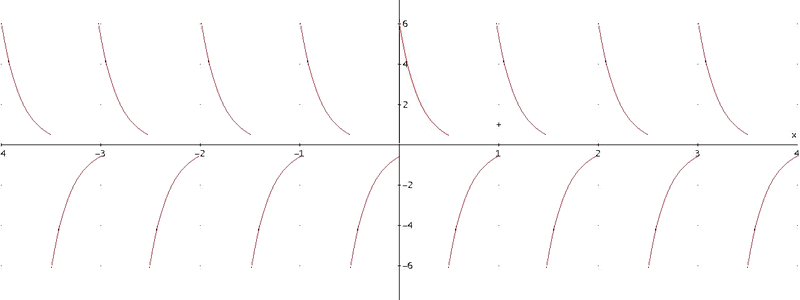
y su representación gráfica:

Archivo:Yt pulsos por exponencial negativa.png

---

Subsección solución 3

Por: Pedro Torruella #04-37657

Para determinar Y(t) también se puede aplicar una forma intuitiva y rápida que es la siguiente.

Si nos olvidamos de la sumatoria y convolucionamos h(t) para una sola delta, obtenemos la misma h(t), luego sabemos que h(t) está definida desde 0 a 0.46 y que cada delta está espaciada una de la otra 0.5, entonces una función no entorpece a la otra y es fácil imaginar cómo se repite la misma función h(t) una y otra vez cambiando de signo junto con las delta.