Matemáticas/Álgebra Abstracta/Apéndices/Funciones

Introducción

En este apéndice, revisamos la noción de función y varias nociones asociadas. No todos los resultados son usados en el texto y están aquí para completitud de la exposición. Ver la sección de Comentarios para algunas observaciones sobre la terminología.

Las Definiciones

Notación y nomenclatura.

1. Una función de $A$ en $B$ se simboliza por $f:A⟶B$. Llamamos dominio o conjunto de partida de la función al conjunto $A$, mientras que el conjunto $B$ es el codominio o conjunto de llegada de $f$. La flecha representa la regla de la función, o sea lo que asigna a cada elemento de $A$ un elemento de $B$.
2. Supongamos que $f$ es una función del conjunto $A$ en el conjunto $B$. Sea $x$ un elemento del conjunto $A$ y sea $y$ el elemento de $B$ asignado por $f$ a $x$. Nos referimos a esa situación por cualesquiera de las expresiones siguientes.
   1. El valor de $f$ en $x$ es $y$.
   2. $f$ envía $x$ en $y$.
   3. La imagen por $f$ de $x$ es $y$.
   4. $f$ asigna a $x$, el elemento $y$.
   5. $f(x)=y$.
3. Supongamos que $f$ es una función de $A$ en $B$. Podemos simbolizar la regla de asignación por $x\mapsto f(x)$. Cuando queramos mencionar el nombre de la función, lo hacemos de una de las dos maneras siguientes: $f:x\mapsto f(x),x\stackrel{f}{\mapsto }f(x).$

   La expresión $f:A⟶B::x\mapsto f(x)$ se lee como "la función $f$ del conjunto $A$ en el conjunto $B$ tal que asigna a cada $x$ de $A$ el elemento $f(x)$ de $B$". Ejemplo: $f:ℝ⟶ℝ::x\mapsto x^2$.

4. Llamamos la imagen de $f$ al subconjunto de $B$ denotado por $\text{im}f$ y definido como el conjunto formado por todos elementos de $B$ que son imagen de algún elemento de $A$. $\text{im}f:=\{y\in B:\text{ hay un }x\in A,f(x)=y\}.$
5. Simbolizamos por $F(A,B)$ al conjunto formado por todas las funciones de $A$ en $B$. En algunos textos, se escribe $B^A$, para denotar a $F(A,B)$.
6. (Igualdad de Funciones.) Decimos que dos funciones, $f$ y $g$, en $F(A,B)$, son iguales, y escribimos $f=g$, ssi, $f$ y $g$ asigna el mismo elemento de $B$ a cada uno de los elementos de $A$. Simbólicamente, $f=g⟺\text{ para todo }x\in A,f(x)=g(x)$.

1. (La función identidad) En cada conjunto $A,$ hay al menos una función del conjunto en si mismo, la función identidad que asigna a cada elemento de $A$ el mismo elemento, a la que simbolizaremos por $1_A$ o $i{d}_A$ o simplemente $id$ (cuando el conjunto es claro del contexto). Es decir tal que $i{d}_A(x)=x.$
2. Sea $A$ un subconjunto de $B$. La relación de inclusión define una función $ı:A⟶B$ tal que $ı(a)=a$. Simbolizamos a esa función por $A\hookrightarrow B.$

---

La clasificación de las funciones

Sea $f:A⟶B$ una función. Dado un elemento $b$ de $B$ consideramos la ecuación

$f(x)=b.$

Las soluciones de esa ecuación son todos los elementos de $A$ cuyas imágenes son iguales al elemento $b$ de $B$. Dependiendo del conjunto solución para esas ecuaciones, tenemos la siguiente clasificación para las funciones.

1. La identidad es una biyección en cualquier conjunto.
   
2. La función definida por la inclusión de un subconjunto es inyectiva, por lo que decimos que se trata de la inyección canónica. Tal función no es suprayectiva, a menos que el subconjunto coincida con el conjunto.
   
3. La función de $ℝ$ en $ℝ$ que asigna a cada número real el cuadrado de dicho número no es ni inyectiva ni suprayectiva, ya que la ecuación $f(x)=4$ tiene dos soluciones y la ecuación $f(x)=-4$ no tiene solución.
   
4. La función de $ℝ$ en ${ℝ}_0^{+}$ (reales positivos junto con el cero) en si mismo que asigna a cada número real su cuadrado es suprayectiva, pero no inyectiva. Ya que, $f(x)=b$ tiene como soluciones a $\pm \sqrt{b}$.
   
5. Sea $A$ un conjunto y $\sim$ una relación de equivalencia en $A$. Simbolizaremos por $\overline{A}$ al conjunto cociente de $A$ respecto a esa relación. La correspondencia que asigna a cada $a$ en $A$ su clase de equivalencia en $\overline{A}$ es una suprayección.
   
6. Sean $A$ y $B$ dos conjuntos cualesquiera. La función de $A\times B$ en $A$ (resp. en $B$) que asigna a cada par $(a,b)$ su primera (resp. su segunda) coordenada es una función suprayectiva, llamada la primera (resp. la segunda) proyección.
   

---

La Composición de Funciones

Observación. Algunas veces tendremos la situación indicada en los diagramas siguientes:

Cuando, en tales diagramas, haya dos "caminos" de un conjunto a otro que representan iguales funciones (por composicion), decimos que el diagrama correspondiente es conmutativo. En el ejemplo anterior, tenemos un triángulo y un cuadrado conmutativo, lo que quiere decir que $h=g\circ f$ y $k\circ h=g\circ f$ respectivamente.

Proposición. La composición, cuando está definida, es asociativa.

Demostración: $\begin{array}{cc}(f\circ (g\circ h))(x)& =f((g\circ h)(x))=f(g(h(x)))\text{, y }\\ ((f\circ g)\circ h))(x)& =(f\circ g)(h(x))=f(g(h(x))).\end{array}$ Plantilla:QED

---

Proposición. Sea $f:A⟶B$ una función entonces:

1. $f\circ 1_A=f$.
2. $1_B\circ f=f$.

Demostración: Trivial. Plantilla:QED

---

La siguiente proposición nos informa acerca de la relación entre la composición de funciones y la "yectividad" de las mismas.

Proposición. La composición de dos funciones inyectivas (resp. suprayectivas, biyectivas) es inyectiva (resp. suprayectiva, biyectiva).

Demostración: Sean $f:A⟶B$, $g:B⟶C$ y $h=g\circ f$.
Caso Suprayectivo. Supongamos que $f$ y $g$ fueran suprayectivas. Debemos probar que para cualquier $c$ en $C$, hay un $x$ en $A$ tal que $h(x)=g(f(x))=c$. Como $g$ es suprayectiva debe haber al menos un $y$ en $B$ tal que $g(y)=c$. Por su parte, como $f$ es suprayectiva, se debe tener que hay un $x$ tal que $f(x)=y$. Luego, $h(x)=g(f(x))=g(y)=c.$

Lo que prueba que la composición es suprayectiva.

Caso Inyectivo. Supongamos que $f$ y $g$ son inyectivas. Sean $x_1$ y $x_2$ elementos de $A$ que tienen la misma imagen por $h$. Entonces,

$\begin{array}{ccccc}& h(x_1)& =& h(x_2)& \\ ⟹& g(f(x_1))& =& g(f(x_2))& \\ ⟹& f(x_1)& =& f(x_2)& g\text{ es inyectiva}\\ ⟹& x_1& =& x_2& f\text{ es inyectiva}\end{array}$

Lo que implica que la composición es inyectiva.

Caso Biyectivo. Sigue de los casos anteriores.

Plantilla:QED

---

La Función Inversa

Proposición. Cuando $f$ tiene inversa, tiene exactamente una única inversa.

Demostración: Sea $f:A⟶B$ y sean $g$ y $h$ inversas de $f$. Entonces, $g=g\circ 1_B=g\circ (f\circ h)=(g\circ f)\circ h=1_A\circ h=h.$ Plantilla:QED

---

Nomenclatura. Cuando exista inversa, por la proposición anterior, dicha inversa será única. Por lo que podremos hablar de LA inversa de $f$, a la que simbolizaremos por $f^{-1}$.

---

Proposición. Cuando la inversa de una función existe, es invertible, y su inversa es la función original.

Demostración: Directo de la definición, ya que $f\circ f^{-1}=i{d}_A\text{ y }f\circ f^{-1}=1_B.$ Plantilla:QED

---

Proposición. La composición de dos funciones invertibles es una función invertible, cuya inversa es la composición de las inversas de las funciones originales, pero en orden inverso.

$(g\circ f{)}^{-1}=f^{-1}\circ g^{-1}.$

Demostración: Sean $f$ y $g$ invertibles. Entonces, $(g\circ f)\circ (f^{-1}\circ g^{-1})=g\circ (f\circ f^{-1})\circ g^{-1}=g\circ g^{-1}=id.$

Análogamente, se verifica que:

$(f^{-1}\circ g^{-1})\circ (g\circ f)=id.$

Por lo tanto, $f^{-1}\circ g^{-1}$ es una inversa de $g\circ f$. Por la unicidad de tales inversas, tenemos el resultado.

Plantilla:QED

---

Proposición. (Criterio para Invertibilidad) Una función es invertible, si, es biyectiva.

Demostración: Sea $f:A⟶B$.
($⟹$) Sea $g:B⟶A$ la inversa de$f$. Sea $b$ en $B$, como $f\circ g=1_b$ se tiene que $f(g(b))=b$, lo que prueba que $f$ es suprayectiva. Supongamos que $f(x_1)=f(x_2)$. Tenemos que $\begin{array}{ccc}f(x_1)=f(x_2)& ⟹& g(f(x_1))=g(f(x_2))⟹1_A(x_1)=1_A(x_2)\\ & ⟹& x_1=x_2.\end{array}$

Lo que prueba que $f$ es inyectiva. Como $f$ es suprayectiva e inyectiva es biyectiva.

($⟸$) Supongamos que $f$ es biyectiva, entonces para cada $b$ en $B$ hay un único elemento $b$ tal que$f(a)=b$. Por lo tanto, la asignación $b\mapsto a$ tal que $f(a)=b$ define una función $g:B⟶A$ tal que $g(f(a))=g(b)=b$. Sea $a$ en $A$, entonces $g(f(a))$ es un elemento $x$ de $A$ tal que $f(x)=f(a)$, por inyectividad, $x=a$; o sea que $g(f(a))=a$. Lo que prueba que $g$ es una inversa de $f$.

Plantilla:QED

---

Proposición. (Propiedades de Cancelación)

1. Las funciones inyectivas son cancelables por la izquierda. Es decir, cuando $f$ es inyectiva se cumple que: $f\circ g=f\circ h⟹g=h.$
2. Las funciones suprayectivas son cancelables por la izquierda. Es decir, cuando $g$ es suprayectiva se cumple que: $g\circ f=h\circ f⟹g=h.$
3. Las funciones biyectivas son cancelables por derecha e izquierda y coinciden con las funciones invertibles.

Demostración: Ejercicio. Plantilla:QED

---

Extensión al Conjunto Potencia

Sea $A$ un conjunto. Simbolizaremos por $\mathbb{P}(A)$ al conjunto potencia de $A$, es decir al conjunto formado por todos los subconjuntos de $A$. Plantilla:DefRht

Observación. Cuando $f$ es una función de $A$ en $B$, algunas veces, se escribe $f(X)$ en lugar de $f_{*}(X)$ y $f^{-1}(Y)$ en lugar de $f^{*}(Y)$. Nosotros usaremos nuestro convenio en el apéndice (pero no en el texto), excepto que la imagen directa de $A$, que coincide con la imagen de $f$ se denotará usualmente por $f(A)$.

---

Proposición. (Propiedades de la Imagen Directa) Sea $f:A⟶B$. Entonces, cuando $X$, $Y$ son subconjuntos de $A$ se cumple que:

1. $X\ne \mathrm{\varnothing }$, ssi, $f_{*}(X)\ne \mathrm{\varnothing }$.
2. $f_{*}(\{x\})=\{f(x)\}$.
3. Si $X\subset Y$ entonces $f_{*}(X)\subset f_{*}(Y)$.
4. $f_{*}(X\cap Y)\subset f_{*}(X)\cap f_{*}(Y)$.
5. $f_{*}(X\cup Y)=f_{*}(X)\cup f_{*}(Y)$.

Demostración: Ejercicio. Plantilla:QED

---

Proposición. Sean $f:A⟶B$ y $g:B⟶C$. Entonces

1. $(g\circ f{)}_{*}=g_{*}\circ f_{*}$.
2. $f_{*}(1_A)=1_{\mathbb{P}(A)}{|}_{f(A)}$.

Demostración: Sea $X\subset A$. Entonces, $z\in (g\circ f{)}_{*}(X)$, ssi, hay un $x$ en $X$ tal que $(g\circ f)(x)=z$, ssi, $g(f(x))=z$, ssi, $z\in g_{*}(f_{*}(X)).$
Plantilla:QED

---

Proposición. (Propiedades de la Imagen Inversa Sea $f:A⟶B$. Entonces, cuando $X^{\prime }$, $Y^{\prime }$ son subconjuntos de $B$ se cumple que:

1. $f^{*}(\mathrm{\varnothing })=\mathrm{\varnothing }$.
2. Si $X^{\prime }\subset Y^{\prime }$ entonces $f^{*}(X^{\prime })\subset f^{*}(Y^{\prime })$.
3. $f^{*}(X^{\prime }\cap Y^{\prime })=f^{*}(X^{\prime })\cap f^{*}(Y^{\prime })$.
4. $f^{*}(X^{\prime }\cup Y^{\prime })=f^{*}(X^{\prime })\cup f^{*}(Y^{\prime })$.
5. $f^{*}(X^{\prime }\setminus Y^{\prime })=f^{*}(X^{\prime })\setminus f^{*}(Y^{\prime })$, cuando $Y^{\prime }\subset X^{\prime }$.

Demostración: Ejercicio. Plantilla:QED

---

Proposición. (Relaciones entre Imágenes Directas e Inversas) Sea $f:A⟶B$. Entonces:

1. $X^{\prime }\subset B⟹f_{*}(f^{*}(X^{\prime }))=X^{\prime }\cap f(A)$.
2. $X\subset A⟹f^{*}(f_{*}(X))\supset X$.

Demostración:
1. Sea $y\in f_{*}(f^{*}(X^{\prime }))$. Entonces, hay un $x$ en $f^{*}(X^{\prime })\subset A$ tal que $f(x)=y$. Por lo tanto, concluimos que: (i) $y$ está en $f(A)$; y (ii) que: $f(x)\in X^{\prime }$, o sea, $y$ está en $X^{\prime }$. Luego, $y$ pertenece a $X^{\prime }\cap f(A)$. Lo que prueba que, $⟹f_{*}(f^{*}(X^{\prime }))\subset X^{\prime }\cap f(A)$. Veamos ahora la inclusión inversa. Sea $y\in X^{\prime }\cap f(A)$. Por lo tanto, $y\in X^{\prime }$ y hay un $x\in A$ tal que $f(x)=y$. Por definición entonces, $x\in f^{*}(X^{\prime })$. Lo que prueba que $y\in f_{*}(f^{*}(X^{\prime }).$
2. Sea $x\in X$, entonces, $f(x)\in f_{*}(X)$. De donde, $x$ está en la imagen inversa de $f_{*}(X)$.
Plantilla:QED

---

Proposición. Sean $f:A⟶B$ y $g:B⟶C$. Entonces

1. $(g\circ f{)}_{*}=g_{*}\circ f_{*}$.
2. $f_{*}(1_A)=1_{\mathbb{P}(A)}$.

Demostración:
1. Sea $X\subset A$. Entonces, $z\in (g\circ f{)}_{*}(X)$, ssi, hay un $x$ en $X$ tal que $(g\circ f)(x)=z$, ssi, $g(f(x))=z$, ssi, $z\in g_{*}(f_{*}(X))$.
Plantilla:QED

---

Proposición. Sean $f:A⟶B$ y $g:B⟶C$. Entonces

1. $(g\circ f{)}^{*}=f^{*}\circ g^{*}$.
2. $f^{*}(1_B)=1_A$.

Demostración:
1. Sea $Z\subset C$. Entonces, $x\in (g\circ f{)}^{*}(Z)$, ssi, $(g\circ f)(x)\in \mathbb{Z}$, ssi, $g(f(x))\in Z$, ssi, $f(x)\in g^{*}(Z)$, ssi, $x\in f^{*}(g^{*}(Z))$.
Plantilla:QED

---

Descomposición Canónica de una Función

Proposición. Sea $f:A⟶B$ una función. La relación definida ${\sim }_f$ definida por $x{\sim }_{f}y⟺f(x)=f(y)$ es una relación de equivalencia.

Demostración: Ejercicio. Plantilla:QED

---

Teorema (Descomposición canónica de una función) Sea $f:A⟶B$ una función. Entonces, podemos factorizar $f$ como:

$f=ı\circ \overline{f}\circ \nu$

donde $\nu :A⟶\overline{A}=A/{\sim }_f$ es la suprayección canónica que envía cada elemento en su clase de equivalencia; $\overline{f}$ asigna $[a]$ el elemento $f(a)$ en $B$ y es una biyección de $\overline{A}$ en la imagen directa de $A$ por $f$, $f(A)$; y, $ı:f(A)⟶B$ es la inyección canónica definida por la inclusión.

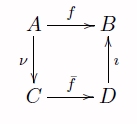
Demostración: Por la proposición anterior ${\sim }_f$ es una relación de equivalencia; por lo que su conjunto cociente está definido. Realmente lo único que necesitamos verificar es que $\overline{f}$ está bien definida y que es una biyección. Notemos que por definición de ${\sim }_f$, si $a^{\prime }$ está en $[a]$ entonces, $f(a^{\prime })=f(a)$; lo que muestra que $\overline{f}$ está bien definida. Es claro además que $\overline{f}$ es suprayectiva. Si $\overline{f}(a)=\overline{f}(a^{\prime })$, se tendrá que $f(a)=f(a^{\prime })$ de donde $[a]=[a^{\prime }]$, probando la inyectividad faltante. Plantilla:QED

---

Comentarios

Terminología. La noción de función es básica en las matemáticas. Funciones aparecen en cualquier área de las matemáticas. No hay, sin embargo, un consenso universal acerca de como referirse a ellas.

Los siguientes nombres han sido usados para denotar funciones:

• Aplicación.
• Mapeo.
• Transformación.
• Operador.

El uso de esos términos obedece a tradiciones (operadores, por ejemplo, para funciones entre espacios de funciones). Siguiendo el peso tradicional, nosotros usamos transformaciones para ciertas funciones en contextos geométricos.

La terminología de "aplicación" y "mapeo" responden más a consideraciones que llamaría folclóricas, es decir, son usadas en ciertos países y en otros no. Algunos autores e instructores usas esa terminología con fines didácticos, usan funciones para contextos numéricos y aplicaciones o mapeos para funciones entre conjuntos que no son numéricos. Es decir el nombre usado depende de la naturaleza de los objetos considerados. En Álgebra Abstracta, el énfasis es en las propiedades de las operaciones abstrayendo (es decir ignorando) la naturaleza de los elementos donde se trabaja. Principalmente, por esa razón hemos usado función en forma uniforme.