Números y Operaciones/Números Racionales B

Números Racionales

En sentido amplio, se llama número racional a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero (una fracción común). El término racional alude a ración o parte de un todo, y no al pensamiento o actitud racional.

Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3). El número racional permite resolver ecuaciones del tipo ax = b, cuando a y b son números enteros (con «a» distinto de cero).

El conjunto de los números racionales se denota por $\mathbb{Q}$ por "Quotient" que significa «cociente» en varios idiomas europeos. Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales. Una pregunta interesante (y muy difícil de resolver) es saber si algunos números más o menos familiares para nosotros como $\pi$, $e$ o $\sqrt{2}$ son números racionales (la respuesta en los casos es NO).

Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relación de equivalencia al conjunto denúmeros fraccionarios.

Historia

En el Antiguo Egipto ya se calculaba utilizando aquéllas cuyos denominadores son enteros positivos, como: cualquier fracción que escribimos con un numerador no unitario, los egipcios la escribían como suma de fracciones unitarias distintas, de ahí que las sumas de fracciones unitarias se conozcan como fracción egipcia. Además, se puede demostrar que cualquier número racional positivo se puede escribir como fracción egipcia. El jeroglífico de una boca abierta (<hiero>D21</hiero>) denotaba la barra de fracción (/), y un jeroglífico numérico escrito debajo de la "boca abierta", denotaba el denominador de la fracción. |} Los babilónicos utilizaban fracciones cuyo denominador era una potencia de 60, mientras que los egipcios usaron, sobre todo, las fracciones con numerador igual a 1. En la escritura, la fracción la expresaban con un óvalo, que significaba parte o partido, y debajo, o al lado, ponían el denominador; el numerador no se ponía por ser siempre 1.

Los griegos y romanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval.

En el siglo XIII Leonardo de Pisa, mejor conocido como Fibonacci, introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.

Construcción de los números racionales

Consideremos las parejas de números enteros $(a,b)$ donde $b\ne 0$ denotado por $\frac{a}{b}$, donde $a$ se le llama numerador y a $b$ se le llama denominador.

Al conjunto de estos números se le denota por $\mathbb{Q}$. Es decir $\mathbb{Q}=\{\frac{p}{q}\mid p\in \mathbb{Z},q\in \mathbb{Z},q\ne 0\}$

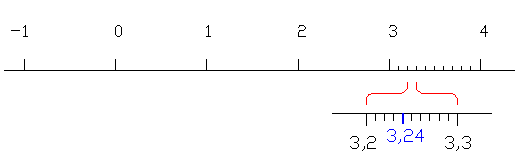
1. Ejemplo de la linea recta con los numeros racionales [1]

Si $p$ es un número entero entonces existe el número $\frac{p}{1}$ que equivale a $p$ y mantiene todas sus propiedades de entero. Es decir, se define ${ℐ}_{\mathbb{Q}}:\mathbb{Z}\mathbb{\to }\mathbb{Q},{ℐ}_{\mathbb{Q}}\left(p\right)=\frac{p}{1}$

• Adición de los Números Racionales

• Multiplicación de los Números Racionales

División de dos numeros racionales

Para dividir dos fracciones, se invierten numerador y denominador de la segunda fracción y luego se procede a multiplicar

$\frac{2}{3}:\frac{6}{5}=\frac{2}{3}\cdot \frac{5}{6}=\frac{2\cdot 5}{3\cdot 6}=\frac{10}{18}=\frac{5}{9}$

• ¿Por qué no podemos dividir por 0?

Relaciones de equivalencia

• Se define la equivalencia $\frac{a}{b}=\frac{c}{d}$ cuando $ad=bc$. Este concepto es importante porque permite explicar por qué hay infinitas maneras de representar un mismo número racional.

Un número racional que es equivalente a dos. Recuerde, hay infinitos racionales que hacen lo mismo

Orden de los Números Racionales

• Los números racionales positivos todos los números de la forma $\frac{a}{b}$ tales que $ab>0$

• Los números racionales negativos son todos los números de la forma $\frac{a}{b}$ tales que $ab<0$

• Se define el orden $\frac{a}{b}>\frac{c}{d}$ cuando $ad-bc>0$

Para números racionales que tienen el mismo denominador hay que comparar los numeradores. La fracción con mayor numerador será mayor.

• Ejemplo:

$\frac{2}{7}$ y $\frac{5}{7}$. La segunda fracción $\frac{5}{7}$ es mayor, ya que $5>2$.

De dos o más números racionales que tienen igual numerador es mayor la que tiene menor denominador.

• Ejemplo:

$\frac{2}{3}$ y $\frac{2}{5}$. La mayor es $\frac{2}{3}$, ya que $3<5$.

Para fracciones con diferente numerador y denominador, se deben buscar fracciones equivalentes hallando el mínimo común denominador (reducir fracciones a común denominador). Para ello, se toma como denominador común el mínimo común múltiplo (mcm) de los denominadores y a partir de ahí estamos en el primer caso que ya hemos visto.

• Ejemplo:

$\frac{1}{4}$ y $\frac{2}{5}$. El mínimo común denominador es 20, resultando $\frac{5}{20}$ y $\frac{8}{20}$. Como $5<8$, $\frac{1}{4}<\frac{2}{5}$.

Notación

• Los números de tipo $\frac{-a}{b}$ son denotados por $-\frac{a}{b}$

• Las sumas de tipo $\frac{a}{b}+\frac{-c}{d}$ son denotadas por $\frac{a}{b}-\frac{c}{d}$

• $\frac{a}{b}\frac{c}{d}$ denota a $\frac{a}{b}\times \frac{c}{d}$

• Todo número $\frac{p}{1}$ se denota simplemente por $p$.

Propiedades de la suma y multiplicación

• La suma en $\mathbb{Q}$ es asociativa, esto es:
  

$\frac{a}{b}+(\frac{c}{d}+\frac{p}{q})=(\frac{a}{b}+\frac{c}{d})+\frac{p}{q}=(\frac{a}{b}+\frac{p}{q})+\frac{c}{d}$

• La suma en $\mathbb{Q}$ es conmutativa, esto es:
  

$\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$

• La multiplicación en $\mathbb{Q}$ es asociativa, esto es:
  

$\frac{a}{b}\times (\frac{c}{d}\times \frac{p}{q})=(\frac{a}{b}\times \frac{c}{d})\times \frac{p}{q}$

• La multiplicación se distribuye en la suma, esto es:
  

$\frac{a}{b}\times (\frac{c}{d}+\frac{p}{q})=(\frac{a}{b}\times \frac{c}{d})+(\frac{a}{b}\times \frac{p}{q})$

Existencia de neutros e inversos

• Para cualquier número racional:

$\frac{a}{b}$ se cumple que $\frac{a}{b}+\frac{0}{1}=\frac{a}{b}$ entonces $\frac{0}{1}$ es el neutro aditivo de los racionales y se le denota por $0$

• Para cualquier número racional:

$\frac{a}{b}$ se cumple que $\frac{a}{b}\times \frac{1}{1}=\frac{a}{b}$ entonces $\frac{1}{1}$ es el neutro multiplicativo de los racionales y se le denota por $1$

• Cada número racional:

$\frac{a}{b}$ tiene un inverso aditivo $\frac{-a}{b}$ tal que $\frac{a}{b}+\frac{-a}{b}=0$

• Cada número racional:

$\frac{a}{b}$, con excepción de 0, tiene un inverso multiplicativo $\frac{b}{a}$ tal que $\frac{a}{b}\times \frac{b}{a}=1$

Otras operaciones de los números racionales

Cuando tenemos una unidad cualquiera, nos puede interesar una parte más pequeña para tomar. Así, si tenemos una tarta para ochos comensales, y estamos cuatro personas, lo normal seria que cada persona tomase dos trozos, expresados así:

$\frac{8}{8}:4=\frac{8}{8}\cdot \frac{1}{4}=\frac{8\cdot 1}{8\cdot 4}=\frac{8}{32}=\frac{8:4}{32:4}=\frac{2}{8}$

Lo que aquí se expresa es que cada persona cogería dos octavos de tarta, es decir, dos partes de las ocho que hay. Así, la parte de arriba (2) seria el numerador, y la parte de abajo (8), el denominador.

Existen situaciones en las que una fracción puede simplificarse dividiendo ambos términos entre un mismo número y resultar ambos valores enteros,

$\frac{12}{4}=\frac{12:2}{4:2}=\frac{6}{2}$

La fracción original y la reducida son equivalentes, esto quiere decir tienen el mismo valor, aunque se escriban diferentes.

Si una fracción tiene términos que ya no se pueden simplificar más se denomina fracción irreducible.

Hallando el máximo común divisor (M.C.D.) de los dos términos y dividiendo ambos términos por él, se llega a una fracción irreducible.

Ejemplo:

Hallar la fracción irreducible de $\frac{12}{4}$:

$M.C.D.(12,4)=4$; dividiendo:

$\frac{12}{4}=\frac{12:4}{4:4}=\frac{3}{1}$

Potenciacion de fracciones

Hay que decir que una potencia es aquella multiplicación donde se multiplica la base por si misma tantas veces como lo indique el exponente. Por lo que es una multiplicación de fracciones.

${\left(\frac{1}{2}\right)}^3=\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}=\frac{1^3}{2^3}=\frac{1}{8}.$

En caso de que la potencia sea negativa, debemos proceder mediante la siguiente fórmula

${\left(\frac{a}{b}\right)}^{-n}={\left(\frac{b}{a}\right)}^n.$

Esto se grafica con el siguiente ejemplo

${\left(\frac{1}{2}\right)}^{-3}={\left(\frac{2}{1}\right)}^3=2^3=2\cdot 2\cdot 2=8.$

Entre las otras propiedades importantes de potenciación tenemos las siguientes

a) Producto de potencias con la misma base:

${\left(\frac{a}{b}\right)}^m\cdot {\left(\frac{a}{b}\right)}^n={\left(\frac{a}{b}\right)}^{m+n}.$

Por ejemplo

${\left(\frac{2}{3}\right)}^3\cdot {\left(\frac{2}{3}\right)}^4={\left(\frac{2}{3}\right)}^{3+4}={\left(\frac{2}{3}\right)}^7=\frac{2^7}{3^7}=\frac{128}{2187}.$

b) División de potencias con la misma base

${\left(\frac{a}{b}\right)}^m:{\left(\frac{a}{b}\right)}^n={\left(\frac{a}{b}\right)}^{m-n}.$

Por ejemplo

${\left(\frac{2}{3}\right)}^3:{\left(\frac{2}{3}\right)}^4={\left(\frac{2}{3}\right)}^{3-4}={\left(\frac{2}{3}\right)}^{-1}=\frac{3}{2}.$

c) Potencia de una potencia

${\left({\left(\frac{a}{b}\right)}^m\right)}^n={\left(\frac{a}{b}\right)}^{mn}.$

Por ejemplo

${\left({\left(\frac{1}{2}\right)}^3\right)}^3={\left(\frac{1}{2}\right)}^9=\frac{1}{512}.$

d) Producto de potencias con el mismo exponente

${\left(\frac{a}{b}\right)}^m\cdot {\left(\frac{c}{d}\right)}^m={\left(\frac{ac}{bd}\right)}^m.$

Por ejemplo

${\left(\frac{2}{3}\right)}^4\cdot {\left(\frac{3}{5}\right)}^4={\left(\frac{2}{5}\right)}^4=\frac{2^4}{5^4}=\frac{16}{625}.$

Radicalización de fracciones

La radicalización es el proceso inverso a la potenciación. Para radicalizar una fracción, se extrae la raiz enesíma al numerador y denominador.

$\sqrt[3]{\frac{8}{27}}=\frac{\sqrt[3]{8}}{\sqrt[3]{27}}=\frac{2}{3}$

$\sqrt{\frac{16}{20}}=\frac{\sqrt{16}}{\sqrt{20}}=\frac{4}{\sqrt{20}}$

Racionalización

En el caso anterior, comprobamos que el denominador tenía una raíz cuadrada en su denominador. Para evitar tal situación, se debe multiplicar la raíz en el denominador consigo misma y por el numerador para así eliminar la raíz.

$\frac{4\cdot \sqrt{20}}{\sqrt{20}\cdot \sqrt{20}}=\frac{4\sqrt{20}}{20}=\frac{\sqrt{20}}{5}$

Existe otro caso en el que el denominador tiene una suma de un número entero con un radical. Para racionalizar, debemos multiplicar por su conjugado (esto es, los mismos elementos pero con el signo cambiado), para así eliminar la raíz del denominador.

$\frac{3-\sqrt{2}}{3+\sqrt{2}}=\frac{(3-\sqrt{2})(3-\sqrt{2})}{(3+\sqrt{2})(3-\sqrt{2})}=\frac{(3-\sqrt{2}{)}^2}{(3+\sqrt{2})(3-\sqrt{2})}=\frac{9+2-6\sqrt{2}}{9-2}=\frac{11-6\sqrt{2}}{7}$

esto no les va a servir es muy malo

Expresión decimal

Es posible expresar una fracción como número decimal dividiendo el numerador entre el denominador:

Ejemplos:

$\frac{1}{2}=1:2=0,5$

$\frac{2}{3}=2:3=0,666...$

En las fracciones con denominador 10, 100, 1000, 10000... se recorrerá el punto hacia la izquierda tantos lugares como cifras cero haya.

• Un número decimal es un número racional de la forma $\frac{a}{10^n}$
• $𝔻$ denota al conjunto de los números de este tipo. Es decir $𝔻=\{\frac{a}{10^n}\mid \frac{a}{10^n}\in \mathbb{Q}\}$
• Expresión Racional de un número decimal: el número $a$ en base $10$ con un punto a $n$ lugares del extremo derecho, por ejemplo $\frac{178}{10^2}$ se denota como $1.78$

Ejemplo

$\frac{53}{1000}=0.053$

$\frac{4}{10}=0.4$

$\frac{4567}{100}=45.67$

Representación decimal de los números racionales

Los números racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:

• Exacta o decimal finito: la parte decimal tiene un número finito de cifras. Ejemplo:

$\frac{8}{5}=1,6$

• Periódica pura o decimal finito periódico: toda la parte decimal se repite indefinidamente. Ejemplo:

$\begin{array}{ccc}\frac{1}{7}& =& 0,142857142857\dots \\ & =& 0,\overline{142857}\end{array}$

• Periódica mixta o decima finito semiperiódico: no toda la parte decimal se repite. Ejemplo:

$\begin{array}{ccc}\frac{1}{60}& =& 0,01666\dots \\ & =& 0,01\bar{6}\end{array}$

En efecto, al aplicar el algoritmo para dividir un entero por otro, sólo existen un número finito de restos posibles. Siendo la sucesión de restos infinita, aparecerá forzosamente un mismo resto en dos posiciones distintas. A partir de ellas, el cálculo se repite igual. Ejemplo:

$\begin{array}{c}0,1428571\dots \\ 7\overline{)10}\\ 30\\ 20\\ 60\\ 40\\ 50\\ 10\\ ⋮\end{array}$

Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera: Léase el artículo entero en Wikipedia:Número Periódico

• Decimales exactos o finitos: Se escribe en el numerador la expresión decimal sin la coma (como un número entero), y en el denominador un uno seguido de tantos ceros como cifras decimales. Ejemplo: $34,65=\frac{3465}{100}$
• Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma, y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. Ejemplo: $15,3434\dots =\frac{1534-15}{99}$
• Decimales periódicos mixtos: Tendrá como numerador la diferencia entre $a$ y $b$, donde $a$ es el número escrito sin la coma, y $b$ es el número sin la parte decimal periódica, escritos ambos como números enteros. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número $12,345676767\dots$ entonces $a=1234567$ y $b=12345$, por lo que el número buscado será $\frac{1234567-12345}{99000}$.

Valor absoluto para números racionales e irracionales

Ya hemos estudiado la función valor absoluto pero trabajar con números racionales e irracionales, aumenta el tipo de problemas y complejiza el estudio que debemos hacer.

Ejemplos

$(a)\left|\frac{1}{2}\right|=\frac{1}{2}.$

$(b)\left|\frac{-3}{5}\right|=\frac{3}{5}.$

$(c)|-\sqrt{3}|=\sqrt{3}.$

$(d)|\frac{1}{2}-\frac{\sqrt{3}}{2}|=\frac{\sqrt{3}}{2}-\frac{1}{2}.$

Esto ocurre pues $\sqrt{3}-1>0.$

$(e)|-\frac{2}{3}+\frac{3\sqrt{3}}{2}+\frac{5}{3}-\frac{\sqrt{3}}{2}|=|1+\sqrt{3}|=1+\sqrt{3}.$

Potencias

Es una forma abreviada de escribir una multiplicación de factores iguales

          base $2^3$exponente

La base corresponde al factor que se repite El exponente indica cuantas veces debe repetirse dicho factor Se lee 2 elevado a 3.

Ejemplo

         $2^3=2x2x2=8$

Potencia en base 10 Toda potencia de base 10 es igual a la unidad seguida de tantos ceros indica el exponente.

Ejemplo

       $10^3=10x10x10=1000$

Multiplicación de potencias de igual base El producto de potencias de igual base es otra potencia de la misma base y cuyo exponente es la suma de sus exponentes.

Ejemplo

       $2^{3}x{2}^{2}x{2}^4=2^{3+2+4}=2^9$

División de potencias de igual base El cociente de dos potencias de igual base es otra potencia de la misma base y cuyo exponente es la resta de los exponentes.

Ejemplo

        $2^6:2^3=2^{6-3}=2^3$

Potencia de una potencia La potencia de una potencia es otra potencia es otra potencia de igual base y cuyo exponente es el producto de los exponentes.

Ejemplo

        $(3^3{)}^2=3^{3x2}=3^6$

Potencia de base fraccionaria y exponente natural Para elevar una fracción a una potenciase eleva tanto el numerador como el denominador al exponente.

Ejemplo

        $(\frac{2}{4}{)}^2=\frac{2}{4}x\frac{2}{4}=\frac{4}{16}$