Trigonometría/Trigonometría

La trigonometría es una rama de las matemáticas que se ocupa del estudio de las relaciones entre los lados y los ángulos de un triángulo. Este estudio da pie a considerar una serie de funciones (seno, coseno, tangente...) que dan lugar a un campo mucho más amplio que el considerado inicialmente y que se aplica sobre todo a fenómenos de tipo periódico, como son las ondas electromagnéticas. En la antigüedad, se uso para los estudios astronómicos y en agrimensura. Hoy en día, además, la trigonometría juega un papel clave en los sistemas de posicionamiento global (GPS).

Conceptos básicos

Identidades trigonométricas fundamentales.

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sen, sin	$\mathrm{sen}\theta \equiv \frac{1}{\csc \theta }\equiv \cos (\frac{\pi }{2}-\theta )\equiv \frac{\cos \theta }{\cot \theta }$
Coseno	cos	$\cos \theta \equiv \frac{1}{\sec \theta }\equiv \mathrm{sen}(\frac{\pi }{2}-\theta )\equiv \frac{\mathrm{sen}\theta }{\tan \theta }$
Tangente	tan, tg	$\tan \theta \equiv \frac{1}{\cot \theta }\equiv \cot (\frac{\pi }{2}-\theta )\equiv \frac{\mathrm{sen}\theta }{\cos \theta }$
Cotangente	ctg (cot)	$\cot \theta \equiv \frac{1}{\tan \theta }\equiv \tan (\frac{\pi }{2}-\theta )\equiv \frac{\cos \theta }{\mathrm{sen}\theta }$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta }\equiv \csc (\frac{\pi }{2}-\theta )\equiv \frac{\tan \theta }{\mathrm{sen}\theta }$
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\mathrm{sen}\theta }\equiv \sec (\frac{\pi }{2}-\theta )\equiv \frac{\cot \theta }{\cos \theta }$

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo: $\alpha$, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

• La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
• El cateto opuesto (a) es el lado opuesto al ángulo $\alpha$.
• El cateto adyacente (b) es el lado adyacente al ángulo $\alpha$.

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa: Plantilla:Ecuación El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo $\alpha$ , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa: Plantilla:Ecuación 3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente: Plantilla:Ecuación 4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto: Plantilla:Ecuación 5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente: Plantilla:Ecuación 6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto: Plantilla:Ecuación

Funciones trigonométricas de ángulos notables

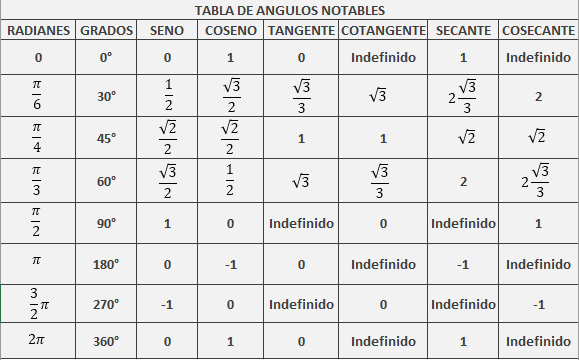
Definición para un número real cualquiera

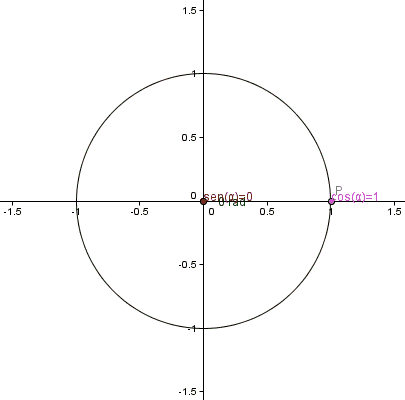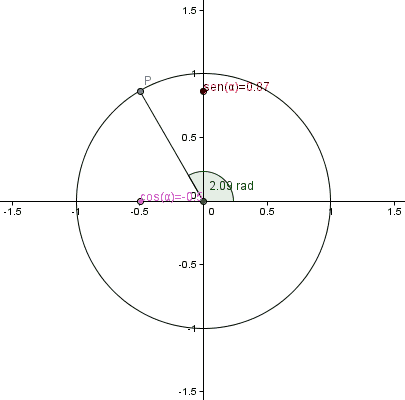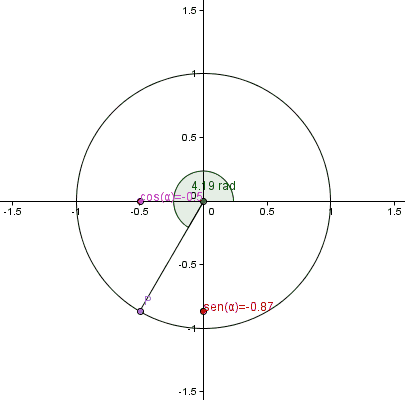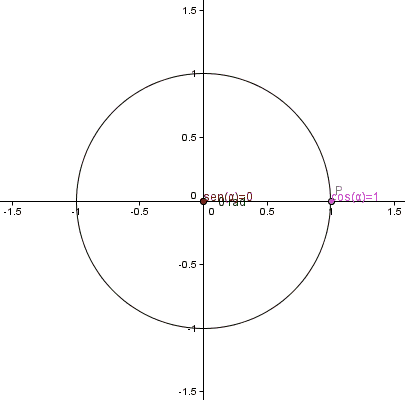
Plantilla:AP No es posible utilizar la definición dada anteriormente, un coseno de $\alpha$ para valores de $\alpha$ menores o iguales a 0 o valores mayores o iguales a π/2, pues no se podría construir un triángulo rectángulo tal que uno de sus ángulos mida $\alpha$ radianes. Para definir los valores de estas funciones para valores comprendidos entre 0 y 2π, se utilizará entonces una circunferencia unitaria, centrada en el origen de coordenadas del plano cartesiano. Se definirán las funciones trigonométricas coseno y seno como la abscisa (x) y la ordenada (y), respectivamente, de un punto P de coordenadas (x, y), perteneciente a la circunferencia, siendo $\alpha$ el ángulo, medido en radianes, entre el semieje positivo x y el segmento que une el origen con P.

Puede observarse que estas funciones toman valores entre -1 y 1. Nótese que para valores entre 0 y π/2, los valores obtenidos para el seno y el coseno con esta definición, coinciden con los obtenidos utilizando la noción de razón trigonométrica. Si el valor de x está fuera del intervalo [0,2π], puede descomponerse como x=2kπ+x' siendo k un número entero y x' un valor entre 0 y 2π. Se asignará a x los mismos valores de seno y coseno que los asignados a x', ya que puede interpretarse a x como un ángulo coterminal con x', y por lo tanto, las coordenadas del punto P serán las mismas en ambos casos.

Representación gráfica

Representación gráfica en un sistema de coordenadas cartesianas.

Teorema fundamental de la trigonometría

${\mathrm{sen}}^2\theta +{\cos }^2\theta =1$

Equivalencia entre las funciones trigonométricas

	Seno	Coseno	Tangente	Cotangente	Secante	Cosecante
$sen\theta$	$sen\theta$	$\sqrt{1-co{s}^2\theta }$	$\frac{tan\theta }{\sqrt{1+ta{n}^2\theta }}$	$\frac{1}{\sqrt{1+co{t}^2\theta }}$	$\frac{\sqrt{se{c}^2\theta -1}}{sec\theta }$	$\frac{1}{csc\theta }$
$cos\theta$	$\sqrt{1-se{n}^2\theta }$	$cos\theta$	$\frac{1}{\sqrt{1+ta{n}^2\theta }}$	$\frac{cot\theta }{\sqrt{1+co{t}^2\theta }}$	$\frac{1}{sec\theta }$	$\frac{\sqrt{cs{c}^2\theta -1}}{csc\theta }$
$tan\theta$	$\frac{sen\theta }{\sqrt{1-se{n}^2\theta }}$	$\frac{\sqrt{1-co{s}^2\theta }}{cos\theta }$	$tan\theta$	$\frac{1}{cot\theta }$	$\sqrt{se{c}^2\theta -1}$	$\frac{1}{\sqrt{cs{c}^2\theta -1}}$
$cot\theta$	$\frac{\sqrt{1-se{n}^2\theta }}{sen\theta }$	$\frac{cos\theta }{\sqrt{1-co{s}^2\theta }}$	$\frac{1}{tan\theta }$	$cot\theta$	$\frac{1}{\sqrt{se{c}^2\theta -1}}$	$\sqrt{cs{c}^2\theta -1}$
$sec\theta$	$\frac{1}{\sqrt{1-se{n}^2\theta }}$	$\frac{1}{cos\theta }$	$\sqrt{1+ta{n}^2\theta }$	$\frac{\sqrt{1+co{t}^2\theta }}{cot\theta }$	$sec\theta$	$\frac{csc\theta }{\sqrt{cs{c}^2\theta -1}}$
$csc\theta$	$\frac{1}{sen\theta }$	$\frac{1}{\sqrt{1-co{s}^2\theta }}$	$\frac{\sqrt{1+ta{n}^2\theta }}{tan\theta }$	$\sqrt{1+co{t}^2\theta }$	$\frac{sec\theta }{\sqrt{se{c}^2\theta -1}}$	$csc\theta$