Dreiecksungleichung (Wiederholung aus der vorhergehenden Lektion)
---
Die Gesamtlänge zweier Seiten eines Dreiecks ist immer größer als die Länge der dritten Seite. Diese Beziehungen lassen sich in der so genannten Dreiecksungleichung ausdrücken.
Nach der Dreiecksungleichung ist im Dreieck die Summe der Längen zweier Seiten a und b stets mindestens so groß wie die Länge der dritten Seite c. Das heißt formal:
Man kann auch sagen, der Abstand von A nach B ist stets höchstens so groß wie der Abstand von A nach C und von C nach B zusammen, oder um es populär auszudrücken: „Der direkte Weg ist immer der kürzeste.“
---
Sind a, b und c die Längen der Seiten eines Dreiecks, so gelten folgende Ungleichungen:
Also gilt:
SATZ:
In jedem Dreieck ist die Summe zweier Seiten größer als die dritte Seite.
---
Der direkte Weg ist immer der kürzeste.
Die kürzeste Verbindung zwischen zwei Punkte ist die Gerade.
BM1702
Kongruenz von Dreiecken
Anwendung des Kongruenzbegriffs auf Dreiecke
kongruent = deckungsgleich
---
Zwei Dreiecke sind kongruent genau dann, wenn es eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
---
Das Dreieck ist das Bild eines Dreiecks bei der Spiegelung an der Geraden .
Die Dreiecke und sind also kongruent.
Wir schreiben: .
BM1703
Bild 1
Bild 2
Eigenschaften kongruenten Dreiecken
--
Die Kongruenz von Dreiecken ist eine Beziehung zwischen jeweils zwei Dreiecken.
Wenn ist, so gibt es eine Bewegung, bei der das Dreieck das Bild des Dreiecks ist.
---
SATZ:
Wenn zwei Dreiecke kongruent sind, dann stimmen sie in den Seiten und in den Winkeln überein.
---
Ein Beweis dieses Satzes ergibt sich durch die Anwendung der Definition für die Kongruenz.
(Definition: Geometrische Figuren heißen kongruent [deckungsgleich] genau dann, wenn es eine Bewegung gibt, die eine Figur auf die andere abbildet.)
Sind nämlich zwei Dreiecke kongruent, so gibt es eine Bewegung, bei der jeder Seite des Originaldreiecks genau ein Seite des Bilddreiecks und jedem Winkel des Originaldreiecks genau ein Winkel des Bilddreiecks zugeordnet ist. Die einander zugeordneten Seiten bzw. Winkel sind dann kongruent. Die beiden Dreiecke stimmen also in den Seiten und in den Winkels überein.
BM1704
Hier nochmals der SATZ aus der vorherigen Übung:
Wenn zwei Dreiecke kongruent sind, dann stimmen sie in den Seiten und in den Winkeln überein.
---
Es gilt auch die Umkehrung des Satzes:
Wenn zwei Dreiecke in den Seiten und in den Winkeln übereinstimmen, dann sind die Dreiecke kongruent.
---
Um diesen Satz zu beweisen, müsste gezeigt werden, dass es auf Grund der in dem Satz genannten Voraussetzugen stets eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen Dreiecks ist.
Wir verzichten an dieser Stelle auf einen Beweis.
BM1705
Bild 1: Gestieltes Laubblatt des Spitz-Ahorns (Acer platanoides)
Bild 2: verschiedene Ebene Vielecke
Unter Planimetrie (von lat. planum für Ebene; und von altgriech. metreo für ich messe; Messung in der Ebene) versteht man allgemein metrische Problemstellungen der ebenen Geometrie, insbesondere die Flächeninhaltsberechnung in der Ebene. (Mit der Flächenberechnung im Raum befasst sich die Stereometrie.)
Der Flächeninhalt einfacher Flächen in der Ebene kann aus bekannten Längenwerten berechnet werden. Die Errechnung komplizierterer Flächen wird meist über Zerlegung in Flächenstücke, die sich leichter errechnen lassen, erreicht. Unregelmäßige Flächen, wie z. B. die Fläche eines Ahornblattes, müssen analytisch mit dem Kurvenintegral – sofern die Kurve analytisch vorliegt – errechnet, mit planimetrischen Methoden abgeschätzt oder planimetriert (ausgemessen) werden.
Dabei zeigt das Beispiel eines Ahornblattes besonders deutlich, dass es um Abstraktion und Näherungsverfahren geht. Planimetrisch berechnet wird nicht die (Ober-)Fläche des (nicht flachen) Ahornblattes, sondern die abstrahierte Fläche, welche seine (mathematisch gedachte) Grundrisszeichnung auf dem Papier einnimmt. Physikalisch allerdings ist auch das Papier nicht flach und die Fläche müsste als Oberfläche stereometrisch berechnet werden, doch da finden sich schon vor der Genauigkeit im Nanobereich riesige Höhlen und Berge, fraktale Klüftungen, dass man darüber fast auf die „Quanten-Frage“ stößt, ob denn die Oberfläche eines Ahornblattes wirklich endlich ist.
BM1706
In der Planimetrie hat man häufig die Kongruenz zweier Dreieck nachzuweisen:
Wir haben dazu zwei Möglichkeiten:
1.) Wir weisen nach, dass es eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
2.) Wir weisen nach, dass die Dreiecke in den Seiten und in den Winkeln übereinstimmen.
Das zweite Verfahren kann vereinfacht werden.
Die drei Seiten und die drei Innenwinkel eines Dreiecks nennt man seine Bestimmungsstücke, kurz Stücke.
---
Zunächst überzeugen wir uns an Beispielen davon, dass zwei Dreiecke im Allgemeinen NICHT kongruent sind, wenn sie nur in
a) einem Stück bzw. b) zwei Stücken übereinstimmen
---
Bild 1
In Bild 1 stimmen die beiden Dreiecke und zwar in den Seiten und überein, sind jedoch nicht kongruent.
---
Die beiden Dreiecke und in Bild 1 stimmen zwar einerseits in den Seiten und sowie andererseits in den Seiten und überein, sind jedoch nicht kongruent.
Der Winkel ist nämlich ein rechter Winkel und der Winkel ein spitzer Winkel.
BM1707
Stimmen zwei Dreiecke in drei Stücken überein, so können sie kongruent sein. Diese Fälle werden wir in den nächsten Übungen untersuchen
---
Kongruenzsatz SWS
---
Seite = S
Winkel = W
SWS: Seite-Winkel-Seite
---
Bild 1
Wir betrachten zunächst den Fall, dass zwei Dreiecke in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen.
Diesen Fall bezeichnen wir mit (sws)
Seite-Winkel-Seite
„Ein Winkel wird von beiden Seiten eingeschlossen“ bedeutet, dass die Seiten auf den Schenkeln des Winkels liegen.
---
Bild 2
Kongruenzsatz (sws):
Zwei Dreiecke, die in zwei Seiten und dem eingeschlossenen Winkel übereinstimmen, sind kongruent.
---
Damit wir sicher sind, dass der Kongruenzsatz (SWS) für alle möglichen Paare von Dreiecken zutrifft, die den Bedingungen (Voraussetzungen ) des Satzes genügen, müssen wir ihn unabhängig von Beispielen beweisen. Wir zeigen dazu, dass es auf Grund der im Satz genannten Voraussetzungen eine Bewegung gibt, bei der das eine Dreieck das Bild des anderen ist.
Der Beweis folgt in der nächsten Übung.
BM1708
Bild 1
Beweis des Kongruenzsatzes (SWS)
---
Für zwei beliebige Dreiecke und seien folgende Bedingungen erfüllt:
---
1.)
Wegen gibt es eine Bewegung, bei der
a) der Punkt Q das Bild des Punktes B,
b) der Strahl QP das Bild des Strahls BA und
c) der Strahl QR das Bild des Strahls BC ist.
2.)
Bei dieser Bewegung ist
a) wegen der Punkt P das Bild des Punktes A und
b) wegen der Punkt R das Bild des Punktes C.
---
Das Dreieck ist also das Bild des Dreiecks bei dieser Bewegung.
Zwei Dreiecke, die in den drei Seiten übereinstimmen, sind kongruent.
---
Kongruenzsatz (ssw)
Zwei Dreiecke, die in den zwei Seiten und dem Gegenwinkel der größeren Seite übereinstimmen, sind kongruent.
BM1711 - BM1720
BM1711
Zeige an je einem Beispiel; dass in den folgende Fällen die beiden Dreiecke nicht kongruent zu sein brauchen:
1.) Zwei Dreiecke stimmen in zwei Seiten und Winkel, der der kleineren Seite gegenüberliegt, überein.
2.) Zwei Dreiecke stimmen in den drei Winkeln überein.
1. Lösung BM1711
Bild 1
Wenn man die Seite, die dem Winkel gegenüberliegt „umklappet“, dann bleibt der Winkel in seiner Größe unverändert. Auch die beiden gegebenen Seiten behalten ihre vorgegebene Länge. Und trotzdem entsteht ein ganz anderes Dreieck.
Beide Dreieck sind nicht mehr deckungsgleich.
Dieser „Trick“ klappt nicht, wenn wie im Kongruenzsatz (ssw) als wichtige Nebenbedinung noch verlangt ist, dass der Winkel der „Gegenwinkel der größeren Seite“ sein soll.
2. Lösung BM1711
Bild 2
Bei zwei Dreiecken mit drei gleichgroßen Winkeln können die Seiten ganz lang oder ganz kurz sein.
Die resultierenden Dreiecke sind sich zwar ähnlich, aber sie sind nicht deckungsgleich (kongruent)
Für kongruente Dreiecke braucht man immer drei Größen.
Aber drei gegebenen Winkel reichen nicht um ein eindeutiges Dreieck zu konstruieren.
Es kann durchaus zwei nicht kongruente Dreiecke geben, die in allen drei Winkeln übereinstimmen.
---
Drei Seiten im Dreieck reichen immer aus, um ein Dreieck eindeutig festzulegen. Stimmen zwei Dreiecke also in allen Seiten überein, so sind sie kongruent.
---
Zwei Seiten und der von ihnen eingeschlossene Winkel reichen auch immer aus, um ein Dreieck eindeutig zu bestimmen.
Achtung: Der Winkel muss eingeschlossen sein, denn sonst sind die Dreiecke meistens mehrdeutig.
---
Dreiecke, die deckungsgleich sind, sind auch immer flächengleich.
Die Umkehrung gilt aber nicht.
Dreiecke, die flächengleich sind, sind NICHT immer deckungsgleich.
---
Ordne die vier Kongruenzsätze für Dreiecke den vier Abbildungen zu!
Bild 2: Wir zeichnen mit einem Zirkel einen Kreis mit dem Mittelpunkt A (blau). Ein Kreisbogen würde auch reichen.
---
Bild 3
Bild 3: Wir zeichnen einen Kreis mit dem Mittelpunkt B (grün). Dieser Kreis muss den gleichen Radius haben wie der erste Kreis mit dem Mittelpunkt A. Die Einstellung des Zirkels darf also nach dem Zeichnen des 1. Kreise nicht verändert werden. Ein Kreisbogen würde auch reichen.
Bild 8: Eine wichtige Bedingung wurde bisher noch nicht erwähnt: Der Radius der beiden Kreise muss ausreichen groß sein. Er muss mindestens so große sein, wie die halbe Länge der gegebenen Strecke. Hier in Abbildung 8 sind die Kreise zu klein, weswegen sie sich nicht schneiden. Folglich kann man mit diesen Kreisen auch keine Mittelsenkrechte zum Halbieren der Strecke konstruieren.
Als zusätzliches Problem ist hier aber die Strecke so lang, dass der zur Verfügung stehende Zirkel zu klein ist, um ausreichend große Kreis zu zeichnen. Die maximal mögliche Größe des Kreise ist der Abbildung zu entnehmen.
Man könnte die Schnittpunkte der kleinen Kreise mit der Strecke verwenden, um sie als Mittelpunkte für weitere Kreise zu nehmen, bis sich die Kreis schließlich doch überschneiden.
1.) Zeichne um den Scheitelpunkt S einen Bogen mit beliebigem Radius. Die Schnittpunkte sind A und B .
2.) Zwei weitere Bögen mit je ausreichendem Radius schneiden sich in einem weiteren Punkt C.
3.) Die Gerade durch S und C halbiert den Winkel.
Hinweis:
Die beiden Bögen um die Punkte A und B müssen den gleichen Radius haben. Dieser darf jedoch vom Radius des Bogens um S abweichen. Je größer die gewählten Radien, um so genauer wird die Konstruktion.
---
Konstruktionsbeschreibung der Winkelhalbierenden:
1.) Wir zeichnen um den Scheitel S einen Kreis mit einem beliebigen Radius und erhalten auf den Schenkeln des Winkels die Punkt A bzw. B.
2.) Wir zeichnen um A und B je einen Kreis mit dem Radius . Die Kreise schneiden einander in einem Punkt, den wir mit C bezeichnen.
Wir zeichnen um A einen Kreis (oder Halbkreis oder Kreisbogen), der die Gerade zu beiden Seiten von A schneidet. Diese beiden Schnittpunkte nennen wir B und C.
Begründe, warum wir sicher sein können, dass wir mit der Konstruktion aus der vorhergehenden Übung die Senkrechte in Punkt A errichtet haben!
1. Lösung BM1719
Begründung:
Die Dreiecke und sind nach Kongruenzsatz (sss) kongruent.
Kannst du das genauer erläutern?
2. Lösung BM1719
Die Dreiecke und sind nach Kongruenzsatz (sss) kongruent, denn
die Strecken und sind gleich lang, ihre Länge ist gleich dem Radius des roten Kreisbogens,
die Strecken und sind gleich lang, ihre Länge ist gleich dem Radius des blauen bzw. grünen Kreisbogens, die laut Konstruktionsanweisung gleich sind.
die Streckn wird von beiden Dreiecken verwendet, sie ist deshalb in beiden Dreiecken gleich lang.
---
Weiter mit der Begründung:
Da dann die Winkel BAD und CAD zueinander kongruente Nebenwinkel sind, ist jeder der beiden ein rechter Winkel.
(Zwei kongruente Nebenwinkel müssen immer 90° große sein.)
Die Gerade DA steht also in Punkt A senkrecht auf der gegebenen Geraden.
(rechter Winkel, senkrecht und 90° bedeuten das gleiche)
BM1720
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
Was ist auf den Abbildungen dargestellt?
Lösung BM1720
Gegeben: Eine Gerade g und ein Punkt Aauf der Gerade.
1.) Markiere mit dem Zirkel von dem Punkt A aus zwei weitere Punkte mit gleichem Abstand zu A auf der Gerade (B, C)
2.) Zeichne um diese Punkte jeweils einen Kreis mit größerem Radius als zuerst mit dem Zirkel abgetragen.
3.) Die Gerade durch A und den Schnittpunkt D der Kreise ist die Senkrechte h zu g im Punkt A und die Mittelsenkrechte der Stecke .
Bild 6
BM1721 - BM1730
BM1721
Bild 1:Zirkel und Lineal
Error al crear miniatura: Bild 2:Die Konstruktion eines regelmäßigen Sechsecks nur mit Zirkel und Lineal
Konstruktion mit Zirkel und Lineal
---
In der euklidischen Geometrie versteht man unter einer Konstruktion mit Zirkel und Lineal die Entwicklung der exakten zeichnerischen Darstellung einer Figur auf der Grundlage vorgegebener Größen, wobei in der Regel nur Zirkel und Lineal verwendet werden dürfen. Das Lineal hat keine Markierungen; man kann damit also nur Geraden zeichnen, aber keine Strecken abmessen.
In der Geometrie werden Zirkel und Lineal auch als euklidische Werkzeuge bezeichnet. Problemlösungen, die auf andere Hilfsmittel zurückgreifen, wurden von den Griechen der klassischen Periode (und auch später von den meisten Geometrietreibenden bis ins 20. Jahrhundert) als nicht zufriedenstellend betrachtet.
---
Euklidische Werkzeuge:
Die Beschränkung auf die „euklidischen Werkzeuge“ leitete sich aus den Postulaten ab, die Euklid am Anfang seines Lehrbuches Die Elemente zusammengestellt hatte. Daraus ergeben sich als einzige zugelassene Anwendungen dieser Werkzeuge:
das Ziehen einer Geraden mit unbeschränkter Länge durch zwei beliebig gegebene, voneinander verschiedene Punkte,
das Ziehen eines Kreises, der einen beliebig gegebenen Punkt als Mittelpunkt hat und durch einen beliebig gegebenen anderen Punkt verläuft, und
das Übertragen bzw. Abschlagen einer Strecke auf einer Geraden oder einer Kreislinie.
Ein Beispiel wäre die Konstruktion eines Dreiecks aus drei Vorgaben, etwa zweier Seiten und eines Winkels.
---
Geschichte:
In der Antike forderte man vorerst kollabierende Zirkel.
(Erläuterung: In den ursprünglichen Konstruktionsproblemen des Euklid wurde von einem kollabierenden Zirkel ausgegangen, dessen Radius beim Hochheben vom Blatt nicht festgehalten werden kann, um einen weiteren Kreis mit diesem Radius zu zeichnen.)
Später war auch der nicht-kollabierende Zirkel für Konstruktionen erlaubt – nicht zuletzt, weil mit Lineal und kollabierendem Zirkel dieselben Punkte konstruiert werden können wie mit Lineal und nicht-kollabierendem Zirkel.
Die Konstruktion nur mittels Zirkel und (unskaliertem) Lineal galt viele Jahrhunderte als die Krone mathematischer Logik. Sie galt aber lange als weitgehend ausgereizt. Die Entdeckung einer Konstruktionsmethode für das regelmäßige Siebzehneck am 29. März 1796 durch Carl Friedrich Gauß war die erste wesentliche Neuerung seit zweitausend Jahren.
Viele Mathematiker haben sich jahrelang an – wie man heute weiß unlösbaren – Aufgaben wie der Quadratur des Kreises versucht.
Nach dem Satz von Mohr-Mascheroni können Konstruktionsaufgaben mit Zirkel und Lineal auch mit dem Zirkel allein ausgeführt werden und nach dem Satz von Poncelet-Steiner auch mit dem Lineal und einem vorgegebenen Kreis.
---
Unmögliche Konstruktionen:
Viele geometrische Figuren können nicht allein mit Zirkel und Lineal exakt konstruiert werden. Darunter sind die klassischen Probleme der antiken Mathematik:
Ein Lot ist in der Geometrie eine Strecke oder Gerade, die auf einer gegebenen Geraden oder Ebene senkrecht steht. Je nachdem, ob es sich um eine Gerade oder um eine Strecke handelt, spricht man auch von Lotgerade oder Lotstrecke. Der Schnittpunkt des Lots mit der gegebenen Geraden oder Ebene wird Lotfußpunkt genannt. Das Lot kann auf verschiedene Weisen mit Zirkel und Lineal geometrisch konstruiert werden.
---
Definition:
Eine Strecke oder Gerade heißt Lot auf eine Gerade , wenn
gilt, wenn sie also senkrecht auf der Geraden oder Ebene steht und somit mit ihr einen rechten Winkel bildet. Der Lotfußpunkt ist dann der Schnittpunkt des Lots mit der Geraden.
BM1723
Geometrische Konstruktionen des Lots
---
In zwei Dimensionen lässt sich das Lot auf eine Gerade auf einfache Weise mit Zirkel und Lineal konstruieren. Je nachdem, ob ein gegebener Punkt auf der Geraden oder außerhalb liegt, spricht man vom Errichten oder vom Fällen des Lots.
Ist ein Punkt auf der Geraden gegeben, dann findet man die Lotgerade durch diesen Punkt wie folgt:
Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines beliebigen Kreisbogens zwei Punkte auf mit gleichem Abstand von . Dann vergrößert man den Winkel des Zirkels, sticht ihn jeweils in einen der beiden gefundenen Punkte auf ein und findet durch Ziehen zweier Kreisbögen einen Punkt (von zwei möglichen) außerhalb der Geraden mit gleichem Abstand von den beiden Punkten. Die Gerade, die durch diesen Punkt und den gegebenen Punkt verläuft, ist dann die Lotgerade zu durch .
Eine Alternative, auf einer Geraden durch den Punkt mit eingeschränkten Platzverhältnissen ein Lot zu errichten, zeigt Bild 2. Die einfache Konstruktion lässt sich auf folgende Art und Weise beschreiben: Man schlägt um einen frei wählbaren Punkt (z. B. eine gedachte Linie von zu bildet mit der Geraden einen Winkel ca. 45°) einen Kreisbogen mit dem Radius , bis er die Gerade in schneidet. Es folgt das Zeichnen einer Linie ab durch , bis sie den Kreisbogen in schneidet. Die abschließende Linie, die durch und verläuft, ist dann die Lotgerade zu durch .
Ist ein Punkt außerhalb der Geraden gegeben, dann findet man das Lot durch auf wie folgt: Man sticht den Zirkel in den Punkt ein und bestimmt durch Ziehen eines Kreisbogens mit entsprechend großem Radius zwei Punkte auf mit gleichem Abstand von . Dann sticht man jeweils in einen der beiden gefundenen Punkte auf ein und findet durch Ziehen zweier Kreisbögen (mit hinreichend großem Radius) einen weiteren Punkt mit gleichem Abstand von den beiden Punkten. Die Gerade, die durch diesen Punkt und den gegebenen Punkt verläuft, ist dann die Lotgerade zu durch und der Schnittpunkt dieser Lotgeraden mit ist der Lotfußpunkt .
Eine alternative Konstruktion (Bild 2), von einem gegebenen Punkt das Lot auf eine Gerade zu fällen, besteht darin, den Zirkel an zwei beliebigen Punkten und auf der Geraden einzustechen und jeweils den Kreis, der durch den gegebenen Punkt verläuft, einzuzeichnen. Diese beiden Kreise schneiden sich dann in einem weiteren Punkt außerhalb der Gerade und die Linie die durch und verläuft, ist dann die Lotgerade durch . Diese Konstruktion kann auch für Spiegelungen benutzt werden.
BM1725
Spiegelung eines Punktes an einer Geraden (Fällen des Lotes)
Gegeben: Eine Gerade g und ein Punkt Paußerhalb der Gerade.
1.) Zeichne um zwei verschiedene Punkte (A , B) der Geraden jeweils einen Bogen vom Punkt P auf die andere Seite.
2.) Der andere Schnittpunkt ist die Spiegelung P' des Punktes P an der Geraden.
3.) Verbinde die Punkte mit einer Geraden. Diese ist das Lot von P auf die Gerade g mit dem Fußpunkt F.
Hinweis:
Die in vielen Lehrbüchern dargestellte Konstruktion mit zwei gleichen Radien ist mathem. nicht notwendig und nur sinnvoll, wenn der Punkt so nahe an der Gerade liegt, dass die Konstruktion zu ungenau wird.
BM1726
Errichten einer Senkrechten zu einer Geraden (Errichten des Lotes)
Zeichne einen unterbrochenen Kreisbogen um den auf der Geraden gewählten Punkt durch den Punkt mit dem Radius . Er schneidet die Gerade in den Punkten und .
Zeichne einen Kreisbogen mit dem Radius , entspricht dem Abstand , um den Punkt bis er den Kreisbogen um in schneidet.
Eine Gerade, deren Punkte von zwei zueinander parallelen Geraden denselben Abstand haben, nennt man Mittelparallele oder Mittellinie dieser parallelen Geraden.
Wenn ein Punkt B auf der Winkelhalbierenden w eines Winkels liegt, dann hat er von den Schenkeln des Winkels gleichen Abstand.
Formal kann man diesen Satz so formulieren:
(Lies: B ist Element von w genau dann wenn gilt: die Strecke BC hat die gleiche Länge wie die Strecke BD.)
---
Beweise diesen Satz!
1. Lösung BM1733
1.) Die Dreiecke und sind kongruent, denn dieser Fall lässt sich auf den Konkruenzsatz (wsw) zurückführen.
---
Erläutere das bitte genauer!
2. Lösung BM1733
1.) Die Dreiecke und sind kongruent, denn dieser Fall lässt sich auf den Konkruenzsatz (wsw) zurückführen.
a) 1. Winkel: (weil Winkelhalbierende)
b) Seite: (die Strecke ist in beiden Dreiecken enthalten)
c) 2. Winkel: (Fußpunkt des Lots)
2.) Folglich sind die Strecken und kogruent, den in kongruenten Dreiecken sind alle Strecken und Winkel kongruent (= deckungsgleich). Der Punkt B hat also von den Schenkeln denselben Abstand.
Gegeben ist der Punkt B, von dem wir dieses mal aber nur wissen, dass er den gleichen Abstand zu den Schenkels eines Winkels hat. (also: )
Jetzt sollen wir beweisen, dass B auf der Winkelhalbierenden liegt.
---
1.) Für die Dreiecke und können wir sagen
a) 1. Seite: (die Strecke ist in beiden Dreiecken enthalten)
b) 2. Seite: (laut Voraussetzung)
c) Winkel: (Fußpunkt des Lots)
2.) Nach dem Konkruenzsatz (ssw) folgt nun, dass die beiden Dreiecke und kongruent sind.
Eine Nebenbedingung für den Kongruenzsatz (ssw) war, dass der Winkel der größeren Seite gegenüber liegt. Diese Bedingung ist erfüllt, denn der besagt Winkel ist 90° und damit der größte Winkel im Dreieck. Dabei müssen wir natürlich wissen, dass der größte Winkel der größten Seite im Dreieck gegenüber liegt. Das hatten wir weiter oben alles schon bewiesen.
2.) Die die Dreiecke und kongruent sind, sind auch die Winkel und kongruent (gleichgroß).
Und schon haben wir damit gezeigt, dass die Strecke die Winkelhalbierende von ist.
leigt demnach auf der Winkelhalbierenden des Winkels .
1.) Wir nehmen an, dass der Schnittpunkt der Mittelsenkrechten der Seiten und eines beliebigen Dreiecks der Punkt sei.
---
2.) Dann gilt einerseits und andererseits .
Daraus folgt: .
---
Leuchtet dir das wirklich ein?
Ich denke, wir sollen beweisen, dass sich alle drei Mittelsenkrechten im Punkt treffen. Warum wird dann plötzlich schon im ersten Punkt angenommen, dass sie sich im Punkt treffen? Ist das nun eine Annahme und damit Voraussetzung oder das Endziel unseres Beweises?
Wenn du es wirklich verstanden hast, dann erkläre es bitte noch einmal mit deinen eigenen Worten, in ganz kleinen Schritten - damit es wirklich jeder versteht!
2. Lösung BM1735
Bild 3
Natürlich sollen wir erst als Endergebnis unseres Beweises zeigen, dass sich alle drei Mittelsenkrechten in einem einzigen Punkt treffen.
Außerdem wird im ersten Satz von „1. Lösung“ nicht davon gesprochen, dass sich die drei Mittelsenkrechten in einem einzigen Punkt treffen, sondern es werden erst mal nur zwei Mittelsenkrechte betrachtet, nämlich und - also die Mittelsenkrechten der Seiten und . Von der Seite ist noch gar keine Rede.
Vorbetrachtung: Wenn wir zwei Geraden haben (in unserem Fall und ), dann sind sie entweder parallel zueinander und schneiden sich deshalb nie. Oder sie sind nicht parallel zueinander und schneiden sich irgendwann zwangsläufig. Und das trifft auch für und zu: Sie müssen sich irgendwo schneiden. Und diesem Schnittpunkt geben wir irgendeinen Namen, damit wir ihn im weiteren Verlauf des Beweises eindeutig und ohne viele Worte benennen können. Wir haben uns für den Namen entschieden. Nichts anderes will uns der erste Satz des Beweises sagen, der da lautete: „Wir nehmen an, dass der Schnittpunkt der Mittelsenkrechten der Seiten und eines beliebigen Dreiecks der Punkt sei.“
Wenn wir nur erst mal die Seite und die Mittelsenkrechte betrachten, dann ist einleuchtend (wir könnten es auch beweisen - verzichten hier aber aus Platzgründen darauf), dass jeder Punkt auf der Mittelsenkrechten (also auch Punkt ) zusammen mit den Endpunkten der Strecke auf die sich die Mittelsenkrechte bezieht ( und ), gemeinsam ein gleichschenkliges Dreieck bildet. In unserem Fall heißen die Endpunkte der Strecke C und B. Wir haben also das gleichschenklige Deieck . Und in diesem gilt, dass die beiden Schenkel gleich lang sind, also: (so wie es im 2. Satz steht).
Nun betrachten wir getrennt die Seite und ihre Mittelsenkrechte . Hier gilt alles, was wir für die Seite a erörtert haben analog auch für Seite .
Der eine oder andere könnte sich jetzt fragen, warum denn die beiden Punkte auf den beiden Geraden und zusammenfallen. Na, das hatten wir doch schon im 1. Satz geklärt, dass es zwangsläufig einen Schnittpunkt der beiden Mittelsenkrechten geben muss und wir ihn auch mit oder benennen könnten.
Wir könnten auch irgendwelche anderen Punkte auf oder auswählen und damit gleichschenklige Dreiecke erhalten. Für uns ist es aber eben interessant den Punkt zu wählen. Sowohl für das gleichschenklige Dreick der Seite , als auch für das gleichschenklige Dreieck der Seite . Noch haben wir damit nicht bewiesen, dass die dritte Mittelsenkrechte () auch durch diesen Punkt geht.
Gut das soll so weit zur Erläuterung des 1. und 2. Satzes unseres bisherigen Beweises reichen.
---
Kannst du den Beweis jetzt selbständig fortsetzen?
Wie weiter oben bereits für die Seiten und erläutert, gilt auch für die Seite , dass ein Punkt (jeder beleibige Punkt) auf der Mittelsenkrechten von (also auf ) ein gleichschenkliges Dreieck mit den Punkten und bildet.
Folglich ist der Punkt also von den Punkten und gleich weit entfernt, wenn er auf der Mittelsenkrechten der Seite liegt.
Mit anderen Worten: Die Mittelsenkrechte von geht ebenfalls durch .
Wir hatten bereits weiter oben gezeigt, dass die Mittelsenkrechten der Seiten und sich in einem gemeinsamen Punkt treffen. Diesen Punkt wollen wir jetzt als bezeichnen. Wir haben die beiden benachbarten Dreiecke und betrachtet und festgestellt, dass es sich um gleichschenklige Dreiecke handelt, bei denen die Schenkel, die von ausgehen alle die gleiche Länge haben.
Nach der gleichen Logik können wir auch die Mittelsenkrechten der Seiten und betrachten. Die Mittelsenkrechten der Seiten und treffen sich ebenfalls in einem gemeinsamen Punkt. Diesen Punkt wollen wir jetzt als bezeichnen. Auch hier haben wir zwei benachbarte gleichschenklige Dreiecke und . Und auch hier haben die Schenkel, die von ausgehen alle die gleiche Länge.
Das gleiche gilt auch, wenn wir die Seiten und betrachten. Die Mittelsenkrechten der Seiten und treffen sich ebenfalls in einem gemeinsamen Punkt. Diesen Punkt wollen wir jetzt als bezeichnen. Und auch hier haben wir zwei benachbarte gleichschenklige Dreiecke und die Schenkel, die von ausgehen, haben alle die gleiche Länge.
Wir haben gezeigt, dass die drei Mittelsenkrechten der benachbarten gleichschenkligen Dreiecke, sich jeweils paarweise in einem gemeinsamen Punkt schneiden.
schneidet sich mit im Punkt
schneidet sich mit im Punkt (also ist )
schneidet sich mit im Punkt (also ist )
Wir halten also fest:
(Diesen Punkt bezeichnen wir einfach al .)
Die Mittelsenkrechten schneiden also einander in Punkt .
In der ebenen Geometrie ist ein Umkreis ein Kreis, der durch alle Eckpunkte eines Polygons (Vielecks) geht.
Nicht für jedes Polygon existiert ein solcher Umkreis. Allgemein besitzt ein konvexes Polygon genau dann einen Umkreis, wenn die Mittelsenkrechten aller Seiten einander in einem Punkt schneiden. In diesem Fall ist der gemeinsame Punkt der Mittelpunkt des Umkreises.
Definition: Es sei ein Dreieck. Ein Kreis, auf dem alle Eckpunkte von liegen, heißt Umkreis von .
Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
Alle Punkte der Mittelsenkrechten zu sind von und gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu übereinstimmende Entfernungen von und . Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken (, und ) gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
Für spitzwinklige Dreiecke liegt der Umkreismittelpunkt im Inneren des Dreiecks. Beim rechtwinkligen Dreieck ist der Mittelpunkt der Hypotenuse (das ist die Seite, die dem rechten Winkel gegenüber liegt) zugleich Umkreismittelpunkt.
Ja, diese drei Punkte liegen auf einem Kreis. Das gilt für beliebige drei Punkte. Drei Punkte bilden ein Dreieck.
Das haben wir gerade in der vorherigen Übung gelernt: Zu jedem Dreieck gibt es einen Umkreis, dessen Mittelpunkt der Schnittpunkt der Mittelsenkrechten ist. Wir betrachten die drei gegebenen Punkte als Ecken eines Dreiecks.
Der Schnittpunkt von zwei Mittelsenkrechten gibt uns berechts den Schnittpunkt M, der auch mit dem Schnittpunkt der dritten Mittelsenkrechten zusammenfällt. Eine dritte Mittelsenkrechte würde uns aber eine Kontrolle erlauben und evtl. die Genauigkeit erhöhen.
Der Schnittpunkt der Mittelsenkrechten () hat von allen Eckpunkten den gleichen Abstand. Dieser Abstand ist der Radius unseres Kreises mit dem Mittelpunkt .
---
Weißt du noch, wie man eine Mittelsenkrechte konstruiert? Erkläre es bitte kurz!
Man konstruiert eine Mittelsenkrechte zwischen zwei gegebenen Punkten und , indem man um diese beiden Punkte mit einem Zirkel Kreisbögen zeichnet mit gleichem Radius, der größer als die halbe Strecke zwischen den beiden Punkten sein muss. Die zwei Schnittpunkte dieser beiden Kreislinien bestimmen eine Gerade. Diese Gerade ist die Mittelsenkrechte der Strecke .
Bild 4: Die Höhe in einem gleichschenkligen Dreieck fällt mit der Mittelsenkrechten und der Winkelhalbierenden zusammen
Höhen des Dreiecks
---
Die Lote , und von den Eckpunkten des Dreiecks auf die gegenüberliegenden Seiten , und oder deren Verlängerungen nennt man die Höhe des Dreiecks.
Die Fußpunkte diese Lote heißen Höhenfußpunkte.
Unter de Länge einer Höhe verstehen wir den Abstand des betreffenden Eckpunktes von der gegenüberliegenden Seite.
BM1738
SATZ:
Die Höhen eines Dreiecks schneiden einander in einem Punkt.
---
Den Beweise für diesen Satz wollen wir mit Hilfe des bereits weiter oben bewiesenen Satzes („Die Mittelsenkrechten eines Dreiecks schneiden einander in einem Punkt.“) führen.
Zum Beweis, dass sich alle drei Höhen des Dreiecks in einem Punkt schneiden, zeichnet man die Parallelen zu den Dreiecksseiten durch die gegenüberliegenden Ecken, sodass ein größeres Dreieck entsteht. Je zwei der vier Teildreiecke des neuen Dreiecks bilden ein Parallelogramm.
---
In einem Parallelogramm sind gegenüberliegende Seiten gleich lang. Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks. Die Höhen des ursprünglichen Dreiecks stimmen daher mit den Mittelsenkrechten des neuen Dreiecks überein.
---
Kannst du das bitte näher erklären! Schritt für Schritt, damit es jeder verstehen kann!
3.) In einem Parallelogramm sind gegenüberliegende Seiten gleich lang.
Definition eines Prallelogramms: Ein Parallelogramm (von griech.„von zwei Parallelenpaaren begrenzt“) ist ein Viereck, bei dem gegenüberliegende Seiten parallel sind.
4.) Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks. Das wollen wir an Seite betrachten - das ist die Seite am kleinen Dreieck, die dem Punkt gegenüberliegt, also von den Punkten und begrenzt wird. Die entsprechende (parallele) Seite am neuen (großen) Dreieck wird von den Punkten und begrenzt. Auch Punkt liegt auf der Geraden . Wir wollen diese Seite des Dreiecks mit bezeichnen.
Nun soll also doppelt so lang sein wie , denn die beiden Teildreiecke 1 und 2 bilden ein Parallelogramm (s.o.), so dass . Außerdem bilden die beiden Teildreiecke 1 und 3 auch ein Parallelogramm, so dass ebenfalls gilt . Wenn wir und zusammen betrachten - das ist unsere Strecke - dann ist doppelt so lang wie . Das ist das, was wir unter 4.) gesagt hatten: „Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks.“
Für die Seite (begrenzt von und ) gilt auch, dass sie doppelt so lang ist wie (begrenzt von den Punkten und ). Dazu müssen wir uns nur das Parallelogramm aus den Teildreiecken 1 und 4 vorstellen und das Parallelogramm aus den Dreiecken 1 und 3.
Das gesagte gilt analog für die Seite (begrenzt von und ), die doppelt so lang ist wie die Seite (begrenzt von und ). (Erstes Parallelogramm aus den Teildreiecken 1 und 2; zweites Parallelogramm aus den Teildreiecken 1 und 4)
5.) Nun zeichnen wir in das große Dreieck Mittelsenkrechte auf allen drei Seiten.
Wir beginnen zuerste mit der Seite . Wir wir bereits gezeigt hatten, liegt Punkt genau in der Mitte, denn zu beiden Seiten von haben die Teilstrecken und die gleiche Länge. Unsere Mittelsenkrechte muss also durch diesen Punkt gehen und senkrecht auf der Seite des großen Dreiecks stehen.
---
Bild 15
Nun zeichen wir noch durch und die Mittelsenkrechten.
Hier sind die drei Mittelsenkrechten des großen Dreiecks mit , und beschriftet.
---
Bild 17
6.) Die Mittelsenkrechten aus dem vorgehenden Bild 16 entfernen wir wieder und zeichnen jetzt stattdessen in das kleine Dreieck die Höhen ein. Zuerst zeichnen wir die Höhe auf der (rot). Diese steht senkrechts auf und geht durch Punkt .
Nun zeichnen wir in das große Dreieck die Mitelsenkrechten ein und in das kleine Dreieck die Höhen. Und siehe da, beiden fallen zusammen. Wie das?
Die Mittelsenkrechten stehen senkrecht auf den Seiten des großen Dreiecks und gehen jeweils durch die Punkte , bzw. . Zufällig stehen sie auch senkrecht auf den Seiten des kleinen Dreiecks, denn die Seiten des großen Dreiecks verlaufen parallel zu den Seien des kleinen Dreiecks.
Auch die Mittelsenkrechten stehen senkrecht auf den Seiten des kleinen Dreiecks (das ist schließlich die Definition für eine Höhe im Dreieck) und senkrecht auf den Seiten des großen Dreiecks, denn die Seiten des großen und kleinen Dreiecks verlaufen parallel zueinander. Also:
7.) Die Höhen des ursprünglichen Dreiecks stimmen mit den Mittelsenkrechten des neuen Dreiecks überein.
8.) Da sich die Mittelsenkrechten eines Dreiecks in einem Punkt schneiden (s. o.: Umkreis), muss dies auch für die Höhen des Ausgangsdreiecks gelten.
Noch mal zum Mitschreiben: Die Mittelsenkrechten des großen Dreiecks schneiden sich. Das ist ein Satz, den wir weiter oben bereits bewiesen haben (Übung BM1735).
Die Höhen des kleinen Dreiecks sind identisch mit den Mittelsenkrechten des großen Dreiecks. Folglich schneiden sich auch die Höhen des kleinen Dreiecks.
Genau das sollten wir beweisen: „Die Höhen eines Dreiecks schneiden einander in einem Punkt.“
w.z.b.w.
BM1739
SATZ:
Der Schnittpunkt der Mittelsenkrechten eines Dreiecks fällt mit dem Schnittpunkt seiner Höhen zusammen.
Natürlich gibt es auch Beispiele, wo der SATZ stimmt. Aber selbst wenn es hundert Beispiele gibt, die zeigen dass der SATZ stimmt, dann ist das noch kein Beweis. Es könnte sich beim 101. Dreieck immer noch erweisen, dass der SATZ nicht richtig ist.
Tausend Beispiele ersetzten keinen Beweis.
Natürlich sind 1000 Beispiele erst mal ein wichtiges Indiz, dass der Satz stimmen könnt und dass man sich an einem Beweis versuchen könnte.
In der vorherigen Übung BM1738 hatten wir doch aber scheinbar gezeigt, dass die Mittelsenkrechten mit den Höhen im Dreieck zusammenfallen. Wo liegt der Denkfehler?
Wir hatten in Übung BM1738 lediglich bewiesen, dass die Mittelsenkrechten des Hilfsdreiecks mit den Höhen des Dreiecks zusammenfallen, nicht aber mit den Mittelsenkrechten des eigentlichen Dreiecks.
BM1740
Bild 1
Bild 1: In das Dreieck wurden die drei Winkelhalbierenden eingezeichnet. Sie treffen sich im einem Punkt (Z). Den Beweis dazu treten wir in einer späteren Übung an (s. u. BM1750).
---
Bild 2
Bild 2: Wenn man einen Kreis mit dem Schnittpunkt der Winkelhalbierenden eines Dreiecks als Zentrum zeichnet (Z), dann erhält man einen Inkreis - wenn der Kreis den entsprechenden Radius hat.
---
Bild 3
Bild 3: Wenn man einen Kreis mit dem Schnittpunkt der Mittelsenkrechten zeichnet (M; blau), dann erhält man den Umkreis. Der Umkreis geht durch alle drei Ecken des Dreiecks.
---
Wenn man einen Kreis mit dem Schnittpunkt der Höhen im Dreieck zeichnet (P; rot), dann erhält man weder einen Innkreis noch einen Umkreis. Dafür kann man aber mit diesen Höhen die Fläche eines Dreiecks berechnen.
BM1741 - BM1750
BM1741
Bild 1: Seitenhalbierende (rot) und Mittelsenkrechte (blau) auf
Bild 3: Seitenhalbierende (rot) und Mittelsenkrechte (blau) auf
Seitenhalbierende
---
Eine Seitenhalbierende (auch Schwerlinie) in einem Dreieck ist eine Strecke, die eine Ecke des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
---
Die Mittelsenkrechte dagegen beginnt zwar auch am Mittelpunkt einer Seite. Sie steht aber immer senkrecht auf dieser Seite und geht nicht zwangsläufig zur gegenüberliegenden Ecke.
---
Bild 4
Die drei Seitenhalbierenden eines Dreiecks sind somit Schwerlinien und schneiden sich in einem Punkt (Q), dem so genannten Schwerpunkt des Dreiecks. (Für den Beweis s. u. Übbung BM1750)
---
Bild 5
Dieser Schnittpunkt der Seitenhalbierenden (S = Schwerpunkt) teilt jede der Seitenhalbierenden im Verhältnis 2:1. Dabei ist die Strecke zwischen Schwerpunkt (S) und Ecke länger als die Strecke zwischen Schwerpunkt und Seitenmittelpunkt.
---
Schwerpunkt:
Würde man eine dreieckige Metallplatte am Schwerpunkt aufhängen, so würde sie waagerecht zum Boden „hängen“.
BM1742
Erkläre den Unterschied zwischen:
1.) Winkelhalbierende
2.) Mittelsenkrechte
3.) Höhe
4.) Seitenhalbierende
Lösung BM1742
1.) Winkelhalbierende: Winkelhalbierende eines Winkels ist die Halbgerade, die durch den Scheitelpunkt des Winkels verläuft und das Winkelfeld in zwei deckungsgleiche Teile teilt.
2.) Mittelsenkrechte: Die Mittelsenkrechte ist eine Gerade, die senkrecht zu einer Strecke verläuft und diese Strecke in der Hälfte teilt.
3.) Höhe: Die Höhe im Dreieck ist die Strecke des Lots von einer Ecke auf die gegenüberliegende Dreiecksseite
4.) Seitenhalbierende: Eine Seitenhalbierende in einem Dreieck ist eine Strecke, die eine Ecke des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet.
---
Ausgezeichnete Punkte im Dreieck = Besondere Punkte im Dreieck
Ausgezeichnete Linien im Dreieck = Besondere Linien im Dreieck
---
Alle vier ausgezeichneten Linien treffen sich jeweils in einem Punkt.
1.) Die Winkelhalbierenden treffen sich im Inkreismittelpunkt I (Schnittpunkt der Winkelhalbierenden).
2.) Die Mittelsenkrechten treffen sich im Umkreismittelpunkt U (Schnittpunkt der Mittelsenkrechten).
3.) Die Höhen treffen sich im Höhenschnittpunkt H (Schnittpunkt der Höhen).
4.) Die Seitenhalbierenden treffen sich im Schwerpunkt S (Schnittpunkt der Seitenhalbierenden).
BM1743
Winkelhalbierende im Dreieck
---
Ist in der Dreieckslehre von Winkelhalbierenden die Rede, so bezieht sich dieser Begriff meist auf die Innenwinkel, seltener auf die Außenwinkel.
Für diese Winkelhalbierenden gelten unter anderem folgende Sätze:
Bild 1
Bild 2
Die drei Winkelhalbierenden (der Innenwinkel) eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Inkreises. (Das sind gleich zwei Aussagen, die wir weiter unten beweisen wollen.)
---
Bild 3
Jede Winkelhalbierende im Dreieck teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten. (Diese Aussage wird auch als Winkelhalbierendensatz bezeichnet. Die genauere Erklärung und der Beweis folgt weiter unten.)
---
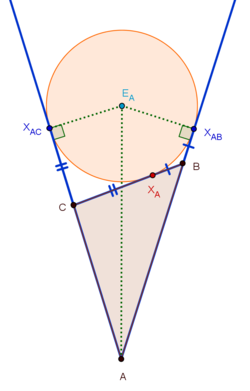
Bild 4
Bild 5
Der Ankreise eines Dreiecks berührt eine Dreiecksseite und die Verlängerungen der beiden anderen Seiten. Es gibt insgesamt drei Ankreis am Dreieck. Die Mittelpunkte der Ankreise ergeben sich dadurch, dass man jeweils die Winkelhalbierende eines Innenwinkels mit den Winkelhalbierenden der nicht anliegenden Außenwinkel schneidet.
---
Die Schnittpunkte der Außenwinkelhalbierenden mit den verlängerten Gegenseiten der entsprechenden Innenwinkel liegen, sofern sie existieren, auf einer Geraden.
BM1744
Dreieck mit Inkreis
Inkreis eines Dreiecks
---
Eine besonders große Bedeutung hat der Inkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Inkreis, sein Mittelpunkt liegt im Schnittpunkt der drei Winkelhalbierenden. Zeichnet man um diesen Schnittpunkt einen Kreis, der eine Seite des Dreiecks berührt (die Seite wird somit eine Kreistangente des Inkreises), so berührt dieser Kreis auch die beiden anderen Seiten.
Alle Punkte der Winkelhalbierenden des Innenwinkels haben den gleichen Abstand von den Seiten und . Entsprechend haben die Punkte der Winkelhalbierenden von den gleichen Abstand von und . Der Schnittpunkt dieser beiden Winkelhalbierenden hat also von allen drei Seiten des Dreiecks (, und ) gleichen Abstand. Er muss also auch auf der dritten Winkelhalbierenden liegen.
Der Inkreis berührt alle drei Seiten von innen – im Gegensatz zu den drei Ankreisen, die jeweils eine Seite von außen und die Verlängerungen der beiden anderen Seiten berühren.
Der Inkreismittelpunkt, also der Schnittpunkt der Winkelhalbierenden, zählt zu den ausgezeichneten Punkten des Dreiecks.
BM1745
Dreieck mit Ankreisen (rot)
Ankreis
---
Die drei Ankreise gehören mit dem Umkreis und dem Inkreis zu den besonderen Kreisen eines Dreiecks, die schon in der Antike von griechischen Mathematikern untersucht wurden.
Die Ankreise sind definiert als Kreise, die jeweils von einer Dreiecksseite von außen und von den Verlängerungen der beiden anderen Seiten tangential berührt werden. Jedes beliebige Dreieck besitzt drei Ankreise. Die Ankreismittelpunkte liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der beiden Außenwinkel, die nicht zu dem Innenwinkel gehören.
Die Ankreismittelpunkte des Dreiecks bilden ein Dreieck, dessen Höhenschnittpunkt der Inkreismittelpunkt des Dreiecks ist.
Eine besonders große Bedeutung hat der Umkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Umkreis, wie im Folgenden begründet wird.
Alle Punkte der Mittelsenkrechten zu sind von und gleich weit entfernt. Entsprechend haben die Punkte der Mittelsenkrechten zu übereinstimmende Entfernungen von und . Der Schnittpunkt dieser beiden Mittelsenkrechten ist also von allen drei Ecken (, und ) gleich weit entfernt. Er muss also auch auf der dritten Mittelsenkrechten liegen. Zeichnet man um diesen Schnittpunkt einen Kreis, der durch eine Ecke des Dreiecks geht, so müssen auch die anderen Ecken auf diesem Kreis liegen.
Der Umkreismittelpunkt, also der Schnittpunkt der Mittelsenkrechten, zählt zu den ausgezeichneten Punkten des Dreiecks.
BM1747
Höhenschnittpunkt
Höhenschnittpunkt
---
Der Höhenschnittpunkt eines Dreiecks ist der Schnittpunkt seiner drei Höhen, d. h. der Lote zu den Dreiecksseiten durch die gegenüberliegenden Ecken. Der Höhenschnittpunkt ist einer der vier klassischen ausgezeichneten Punkte des Dreiecks.
In der Skizze sind die Höhen mit [AHa], [BHb] und [CHc] bezeichnet. Ist das gegebene Dreieck ABC spitzwinklig, so befindet sich der Höhenschnittpunkt H innerhalb des Dreiecks. Hat das Dreieck dagegen einen stumpfen Winkel (also einen Winkel über 90°), so liegt H außerhalb. Im rechtwinkligen Fall schließlich stimmt H mit dem Scheitel des rechten Winkels überein.
BM1748
Fagnano-Problem
---
Das Fagnano-Problem ist das folgende nach Giovanni Fagnano benannte Optimierungsproblem.
Bestimme das in ein spitzwinkliges Dreieck einbeschriebene Dreieck minimalen Umfangs.
Hierbei versteht man unter einem einbeschriebenen Dreieck eines Dreiecks ein Dreieck , dessen Ecken auf den Seiten Dreiecks liegen, das heißt , und . Für das Höhenfußpunktdreieck gilt, dass sein Umfang geringer ist als der eines jeden anderen einbeschriebenen Dreiecks und somit ist es die Lösung des Fagnano-Problems.
Unter allen Dreiecken, die einem spitzwinkligen Dreieck einbeschrieben sind, hat das Höhenfußpunktdreieck den kleinsten Umfang.
---
Bild 2: Höhenfußpunktdreieck
Das Höhenfußpunktdreieck ist ein Begriff aus der Dreiecksgeometrie. Es entsteht dadurch, dass die Fußpunkte der drei Höhen (also die Punkte , und , in denen die Lote von den Ecken des Dreiecks auf die gegenüber liegenden Seiten diese Seiten schneiden) miteinander verbunden werden.
BM1749
Feuerbachkreis
---
Der Feuerbachkreis oder Neun-Punkte-Kreis ist ein besonderer Kreis im Dreieck, der nach Karl Wilhelm Feuerbach benannt ist. Auf ihm liegen neun ausgezeichnete Punkte:
die Mittelpunkte der Seiten;
die Fußpunkte der Höhen;
die Mittelpunkte der oberen Höhenabschnitte (das sind die Mittelpunkte der Strecken zwischen jeweils einer Dreiecksecke und dem Höhenschnittpunkt des Dreiecks).
Im Bild rechts sind D, E und F die Seitenmittelpunkte, G, H und I die Höhenfußpunkte, J, K und L die Mittelpunkte der oberen Höhenabschnitte und S der Höhenschnittpunkt.
BM1750
Bild 1
Winkelhalbierende
---
SATZ:
Die Winkelhalbierenden eines Dreiecks schneiden einander in einem Punkt.
---
Wie kann man das beweisen?
Lösung BM1750
Bild 2
sei der Schnittpunkt der Winkelhalbierenden und eines beliebigen Dreiecks .
Dann hat einerseits von den Seiten und sowie andererseits von den Seiten und denselben Abstand.
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
_Circumscribed.svg){kind=link}
_Circumscribed.svg){kind=link}
_Circumscribed.svg){kind=link}
